Riemann widerlegt Euler: Hintergrund einer weltbewegenden wissenschaftlichen Entdeckung

Der folgende Text ist die Einleitung zur englischen Erstübersetzung einer Sammlung von Schriften Bernhard Riemanns, die in der Winter-Ausgabe 1995 des Magazins 21st Century Science & Technology erschienen ist. Die deutsche Übersetzung ist von Dr. Wolfgang Lillge.

---

Auf den folgenden Seiten veröffentlicht 21st Century die erste bekannte englische Übersetzung einer Reihe posthum veröffentlichter früher Schriften des berühmten Physikers Bernhard Riemann (1826–1866).¹ Deren besondere Bedeutung liegt darin, daß sie den unverzichtbaren Hintergrund liefern, um zu verstehen, wie Riemann zu seinen weltbewegenden Entdeckungen der Zeit von 1853–1854 kam.²

Die besondere Bedeutung dieser Schriften liegt außerdem in dem Umstand, daß sich Riemanns Werk nicht kompetent würdigen läßt, ohne seine Schriften (und auch die von Karl Weierstrass) als vernichtende Widerlegung von Leonhard Eulers wüsten Angriffen auf Gottfried Wilhelm Leibniz zu verstehen.³ Im Rahmen einer Diskussion über mathematische Reihen geht es hierbei formal um die Frage, ob es mathematische Unstetigkeiten gibt oder nicht.⁴ Die entscheidende inhaltliche Frage hinter den Angriffen auf Leibniz durch die Newtonianer des 18. Jahrhunderts wie Dr. Samuel Clarke und Leonhard Euler ist heute noch mehr als zu Riemanns Zeit, ob die Physik ein Zweig der Mathematik oder die Mathematik ein Zweig der Physik ist.

Vor allem im Schlußsatz seiner berühmten Habilitationsschrift von 1854 zeigte Riemann auf, daß man zur Lösung der Grundfragen der Mathematik den Bereich der Mathematik verlassen und zur Physik überwechseln müsse.⁵ Mit dieser Äußerung stehen Riemann wie auch sein Lehrer Gauß vor ihm voll und ganz im Bereich der Physik, im Gegensatz zu dem Einfluß, den Bertrand Russell und Bourbakis Golem auf einen Großteil der mathematischen Lehre ausüben. Die posthum veröffentlichten Schriften beleuchten direkt, wie sich Riemanns Herangehensweise zu dieser Frage entwickelte.

Riemann und Wirtschaft

Die Beachtung, die 21st Century Riemann schenkt, ist Ausdruck meiner eigenen ursprünglichen Arbeit in einem von Leibniz begründeten Zweig der Physik, der auch als physische Ökonomie bekannt ist. Meine Entdeckungen in diesem Bereich gaben den Hauptanstoß für die Gründung der Fusion Energy Foundation Mitte der 1970er Jahre, die dann die Herausgabe des Magazins 21st Century nach sich zog. Riemanns Arbeit gab zwar nicht den Anstoß für den Hauptteil meiner Entdeckungen, doch der Ansatz zur Lösung der mathematischen Probleme, die sich durch diese Entdeckungen stellten, hatte seinen Ursprung fast vollständig in Riemanns Habilitationsschrift, was auch zu der Bezeichnung „LaRouche-Riemann-Methode“ führte.⁶

Zur Einführung in Riemanns posthum veröffentlichte Schriften weise ich auf jene Aspekte seiner Habilitationsschrift hin, die für die Probleme der physischen Ökonomie am relevantesten sind. Hierzu betrachte man zuerst den Rang, den mathematische Unstetigkeiten in Riemanns Entdeckung einnehmen, und dann die Bedeutung dessen, was Riemann in seinen posthum veröffentlichten Schriften als Geistesmassen bezeichnet.

Um zunächst die Bedeutung mathematischer Unstetigkeiten zu definieren, formuliere ich in eigenen Worten, wovon Riemann in seiner Habilitationsschrift ausgeht.

Der Ursprung der modernen Mathematik liegt in dem, was man gewöhnlich als einfache „Euklidische“ Raumzeit bezeichnet. Diese Raumzeit gibt vor, das reale Universum zu repräsentieren, was aber nicht der Fall ist. Sie ist eine Vorstellung, die kein Produkt der Sinne, sondern der naiven Imagination ist. Wir stellen uns lediglich vor, daß der Raum durch drei Richtungssinne (rückwärts-vorwärts, aufwärts-abwärts, seitwärts-seitwärts) definiert ist, und meinen, diese ließen sich unbegrenzt und in vollkommen unterbrechungsfreier Stetigkeit erweitern. Wir stellen uns vor, die Zeit sei eine einzelne, unbegrenzte Dimension vollkommener Stetigkeit: vorwärts-rückwärts. Zusammengenommen definieren diese Annahmen eine vierdimensionale Raumzeit-Mannigfaltigkeit oder, anders ausgedrückt, eine vierfach ausgedehnte Raumzeit-Mannigfaltigkeit.

Die naive Imagination versucht, wahrnehmbare Körper und ihre Bewegungen in einer solchen vierfach ausgedehnten Mannigfaltigkeit zu lokalisieren. Man könnte auch sagen, unsere angenommene Raumzeit-Mannigfaltigkeit dient als eine Art geistiger Spiegel, auf den wir Reflexionen der Bewegung von Körpern in der Raumzeit zu projizieren versuchen. Das Ergebnis solcher Projektionen ist eine einfache „Euklidische“ Art der algebraischen Mathematik, die, wie man schnell feststellt, keine Mathematik des realen Universums ist.

Klassische Experimente wie die Messung der gekrümmten Erdoberfläche durch Eratosthenes von der Platonischen Akademie⁷ sind der meßbare Beweis dafür, daß die Bewegung von Körpern in der physikalischen Raumzeit nicht dem entspricht, was eine naive, algebraische Vorstellung von Raum vermuten läßt. Man muß nicht-raumzeitliche „Dimensionen“ wie „Masse“, „Ladung“ usw. hinzunehmen, um zu einer Mathematik zu gelangen, die mit unserer Messung der Bewegungen übereinstimmt, welche sich aus der physikalischen Raumzeit auf dem imaginären Spiegel reflektieren, der als einfache Raumzeit bekannt ist.⁸

Es geht also nicht um eine vorgestellte vierdimensionale Raumzeit, wenn man die physikalische Raumzeit zu erkunden versucht, sondern um eine physikalische Raumzeit-Mannigfaltigkeit von viel mehr Dimensionen als den vier Dimensionen der naiven Raumzeit. Man nennt diese zusätzlichen Faktoren „Dimensionen“, denn sie lassen sich entsprechend dem Ordnungsprinzip „größer als“ und „kleiner als“ skalieren, wie es auch mit den Dimensionen der naiven Raumzeit geschieht. Anstatt von n + 4 Dimensionen zu sprechen, bezieht man die Vier in die Zählung von n ein; man spricht deshalb von einer „physikalischen Raumzeit-Mannigfaltigkeit von n Dimensionen“. Dann versucht man gewöhnlich, die Bewegung innerhalb dieser physikalischen Raumzeit von n Dimensionen entsprechend ihrer imaginären Reflexion auf eine vierdimensionale Raumzeit darzustellen.

Jedesmal, wenn der physikalischen Raumzeit-Mannigfaltigkeit eine verifizierbare neue „Dimension“ hinzugefügt wird, entspricht dies einer Meßwertänderung, einer Änderung in dem Maßstab, den wir für die Messung der betreffenden Bewegung oder einer entsprechenden Wirkungsform anlegen müssen. Eratosthenes hatte zum Beispiel berechnet, daß die Erde ein Sphäroid von etwa 13.345 km von Pol zu Pol sei (keine schlechte Schätzung für die damalige Zeit).⁹ Das bedeutet, um eine Bewegung entlang der Erdoberfläche zu messen, muß man den Maßstab der sphärischen Trigonometrie anlegen, und nicht den, den man für eine einfache Euklidische Ebene verwenden würde. Denn sobald etwa Ole Rømer 1676 gezeigt hatte, daß die Ausbreitung des Lichts nach dem Prinzip eines retardierten Potentials erfolgt, konnte Christian Huygens 1677 die Reflexions- und Brechungsgesetze entsprechend generalisieren,¹⁰ und Johann Bernoulli und Leibniz bewiesen, daß an die Stelle der algebraischen Methoden von Galileo, Descartes und Newton eine transzendente Mathematik der speziellen Relativität treten müsse.¹¹

Um den notwendigen Zusatz einer solchen weiteren physikalischen Dimension durch Messung zu bestätigen, muß hier eine weitere Forderung betrachtet werden. Ein jeder solcher Zusatz bedeutet, daß n durch (n+1) anstatt durch eine n-fache physikalische Raumzeit-Mannigfaltigkeit ersetzt wird. Dadurch erhält man einen generalisierten Topologie-Ausdruck, der sich symbolisch durch (n + 1)/n darstellen läßt. Die Veränderungsreihe von n– zu (n + 1)-Dimensionen ist mit einer Veränderungsreihe in der Wahl des Maßstabs verbunden, der verwendet werden muß, um den betreffenden physikalischen Vorgang zu messen.¹²

Mit dem gleichen Problem haben wir es auch in der physischen Ökonomie zu tun, wenn man versucht, die Beziehung zwischen wissenschaftlichem und technologischem Fortschritt auf der einen Seite mit der daraus resultierenden allgemeinen Erhöhung der produktiven Arbeitskraft pro Kopf, pro Haushalt und pro Quadratkilometer auf der anderen Seite zu definieren. In diesem Fall nennt sich der zu benutzende Maßstab potentielle relative Bevölkerungsdichte. Dieser Maßstab verändert seine Skalierung (pro Kopf, pro Quadratkilometer), wenn die Höhe des angewandten wissenschaftlichen und technologischen Fortschritts ansteigt.

Wissenschaft und Metapher

Die in Riemanns Habilitationsschrift aufgeworfenen Fragen sind zwar äußerst tiefgreifend, aber gleichzeitig auch so elementar, daß sie von einem guten Abiturienten verstanden werden können. Sobald man seiner darin geäußerten Absicht zustimmt, erscheint diese Schrift als eines der klarsten Prosastücke, die jemals in das Schrifttum wissenschaftlicher Grundlagenentdeckungen Eingang gefunden haben. Zugegebenermaßen haben die meisten der vermeintlich maßgeblichen Kommentatoren eine gegensätzliche, konfuse Meinung zu diesem Werk abgegeben. Der Fehler all dieser Meinungen liegt darin, daß die Kommentatoren, indem sie sich weigern, die Tatsache von Riemanns Aussage zu akzeptieren, auf ihn eine Absicht projizieren, die der seinigen ganz grundlegend entgegenläuft.

Der Grundfehler dieser maßgeblichen Kommentatoren bewegt sich auf zwei Ebenen.

Näher an der Oberfläche versuchen sie, mathematische Autoritäten wie Newton, Euler, Augustin Cauchy u. a. vor der vernichtenden Widerlegung in Schutz zu nehmen, die aus Riemanns Entdeckung folgt. Dabei geht es vor allem um Eulers Einwendungen gegen Leibniz. In dieser relativ oberflächlichen Behauptung bestehen die Positivisten darauf, daß es letztlich keine mathematischen Unstetigkeiten gibt.¹³

Auf tieferer Ebene geht es um eine vernichtendere Frage, über die die Gegner von Leibniz und Riemann nicht zu debattieren wagen.

Die Radikalpositivisten des Bourbaki-Kults sind exemplarisch für diese tiefere Frage. Der absonderliche, Ockhamistische Götterglaube dieser positivistischen Ideologen ist das Dogma, daß sämtliche Wissenschaftsfragen durch mathematische Beweise entweder an der Tafel oder mit einem modernen Computersystem entschieden werden müssen. Sobald jemand aufzeigt, daß mathematischer Formalismus nicht der Gott der Wissenschaft ist – entweder durch Platon und seine Akademie nach ihm oder in der Moderne durch Leibniz oder Riemann – erfüllt dies die Positivisten mit einer ordinären, irrationalen Wut, die in Geist und Denken der des jakobinischen Mobs von Marat oder Danton gleichkommt.

Diese tiefere Ebene fundamentaler Fragen war ausschlaggebend dafür, daß der Abt Antonio Conti seinen Agenten Dr. Samuel Clarke damit beauftragte, Leibniz zu attackieren. Diese Frage liegt auch den wilden, posthumen Angriffen auf Leibniz durch Euler und die Conti-Salons zugrunde. Genauso war dies der Grund dafür, daß die Anhänger Ernst Machs in der Zeit des Ersten Weltkriegs wie die Hyänen über Max Planck herfielen.¹⁴

Sobald man der primären historischen Tatsache mathematisch-physikalischer Erkenntnis zustimmt, daß alle diese grundlegenden physikalischen Entdeckungen, die durch geeignete Messungen bestätigt wurden, der Mathematik die topologische Aufgabe der erwähnten Form (n + 1)/n stellen, verliert der mathematische Formalismus jene gottähnliche Autorität, die die Anhänger Eulers und des Bourbaki-Kults so fanatisch verfechten.¹⁵ Wie Leibniz vor ihm zeigte Riemann mit seiner Entdeckung, daß der mathematisch-physikalische Formalismus nicht die Anforderungen einer Wahrheitslehre erfüllt. Um die Wahrheit zu finden, müssen wir den Bereich der Mathematik verlassen und uns in einen anderen Bereich begeben, das Gebiet der Experimentalphysik.

Entscheidend bei all dem und abgeleiteten formalen Fragen der mathematischen Physik ist der Zusammenhang zwischen der irrigen Annahme, daß es in der Mathematik letztlich keine Unstetigkeiten gibt, und der tieferen (ebenso falschen) Annahme, die unter den Anhängern des Bourbaki-Dogmas vorherrscht, daß die Mathematik eine Wahrheitslehre sein könne.

Es ist zulässig zu sagen, daß jede schlüssige mathematische Physik einer bestimmten n-fachen physikalischen Raumzeit-Mannigfaltigkeit als ein formales, deduktives Theoremgitter verstanden werden kann. In dieser Interpretation zeigt sich, daß sich jedes Theorem dieses Gitters durch die Eigenschaft auszeichnet, eine Aussage zu sein, die sich als nicht im Widerspruch stehend zu jeder Axiomen- und Postulatenreihe erwiesen hat, die diesem Gitter als Gesamtheit zugrundeliegt.¹⁶ Eine solche Reihe von Axiomen und Postulaten wird von Platon wie von Riemann als Hypothese bezeichnet, im Gegensatz zu der mißbräuchlichen Verwendung des gleichen Begriffs in Newtons berühmten Ausspruch „et hypotheses non fingo“.¹⁷

Ein kenntnisreicher Gebrauch des Begriffs „Hypothese“ ist bereits zum Verständnis der Überschrift von Riemanns Habilitationsschrift unabdingbar, noch bevor man zum eigentlichen Text übergeht. Für ein kundiges Verständnis von Riemanns Habilitationsschrift ist entscheidend, daß eine topologische Transformation wie bei dem Übergang von einer mathematisch n-fachen physikalischen Raumzeit-Mannigfaltigkeit zu einer Mannigfaltigkeit von (n + 1)-Dimensionen eine Transformation in der der mathematischen Physik zugrundeliegenden Reihe von Axiomen und Postulaten ist.

Somit eröffnet uns die Geschichte der Entdeckungen physikalischer Prinzipien, die – wie Eratosthenes‘ Berechnung der Erdkrümmung – durch entsprechende Messungen bestätigt wurden, eine Abfolge topologischer Veränderungen, die die Form des Paradoxes vom „Einen“ und „Vielen“ in Platons Parmenides haben. In diesem Fall wird das „Viele“ durch eine Reihe von Hypothesen dargestellt; die Herausforderung ist, ein höheres Prinzip zu entdecken, eine höhere Hypothese, das „Eine“, das ein Erzeugungsprinzip definiert, mit dessen Hilfe die Reihe von Hypothesen, das „Viele“, „transfinit“ geordnet wird. Wenn man Riemanns Habilitationsschrift auf irgendeine andere Weise versteht als in diesem platonischen Sinn, sind die sich daraus ergebenden Kommentare über den Text wissenschaftlich unbedarft, ganz gleich welches Renommee der Kommentator haben mag.

Riemann vertritt eine Sichtweise der mathematischen Physik, die auf der Abfolge von Fortschritten in der Entdeckung physikalischer Prinzipien basiert, die durch entsprechende Messungen bestätigt wurden, so wie Eratosthenes‘ Berechnung der Erdkrümmung ein solches Meßprinzip verkörpert. Riemanns Verständnis dieser topologischen Transformation, die dem Fortschritt der mathematischen Physik zugrundeliegt, definiert somit Fortschritt in der mathematischen Physik als eine Abfolge absoluter mathematischer Unstetigkeiten innerhalb eines formalistischen Verständnisses der mathematischen Physik selbst. So lassen sich beispielsweise Newton, Euler und Cauchy als Opfer ihrer eigenen wissenschaftlichen Unbedarftheit verstehen, als Opfer eines ontologischen Paradoxes vom „Einen“ und „Vielen“, das sie weder lösen konnten noch verstanden haben – und offenbar auch gar nicht verstehen wollten.

Ein formales Theoremgitter unterscheidet sich jeweils von einem anderen durch jegliche Veränderung im axiomatischen Inhalt, von dem der einen zugrundeliegenden Hypothese zu dem der anderen zugrundeliegenden Hypothese; jedes Theorem des zweiten Gitters ist formal widersprüchlich zu jedem Theorem des ersten. Der Unterschied zwischen den beiden Hypothesen ist eine wirkliche und relativ absolute mathematische Unstetigkeit. Eine solche „Unstetigkeit“ hat in der mathematischen Physik die gleiche Bedeutung wie der richtig verstandene Begriff „Metapher“ in klassischen Formen von Poesie oder Drama. Was „Unstetigkeit“ bezüglich der Formalitäten einer konsistenten mathematischen Physik bedeutet, ist genau das, was „Metapher“ für ein klassisches Gedicht oder Drama bedeutet.¹⁸ Die Beziehung zwischen Metapher und mathematischer Unstetigkeit zu verstehen, ist der Kern von Riemanns posthum erschienener Schrift „Zur Psychologie und Metaphysik“.

In der Physik erscheint eine mathematische Unstetigkeit als bloßes Zeichen. Die Größe dieses Zeichens ist von transinfinitesimaler Kleinheit, so klein, daß es mit keiner berechenbaren arithmetischen Größe bemessen werden kann; dennoch existiert es als Phänomen: offenbar als Trennmarkierung von allen Größen, die kleiner sind, von allen Größen, die größer sind.¹⁹ Dieses Zeichen bedeutet außerhalb des Bereichs mathematischer Formalitäten die mathematisch-physikalische Form dessen, was man in der klassischen Poesie als Metapher kennt.

Riemanns „Geistesmassen“

Die Tatsache, daß alle wirklichen Metaphern Singularitäten sind, ist der Schlüssel, um wirklich zu verstehen, wie Riemann in der ersten seiner posthum veröffentlichten Schrift „Zur Psychologie und Metaphysik“ den Begriff der „Geistesmassen“ benutzt. Zur Verdeutlichung des Prinzips, um das es hier geht, betrachte man das Beispiel der Metapher entweder in einem klassischen strophischen Gedicht oder in einem solchen von Mozart,²⁰ Beethoven, Schubert, Schumann oder Brahms²¹ vertonten Gedicht. Das Beispiel des klassischen strophischen Gedichts und seine Vertonung entsprechend den Prinzipien der Motivführung ist für das Verständnis der geistigen Prozesse entscheidend, mit deren Hilfe eine verifizierbare Entdeckung neuer wissenschaftlicher Prinzipien erzeugt werden.²² Dies ist auch ein Beispiel für das Konzept, das sich durch Platons Behandlung des ontologischen Paradoxes des „Einen“ und „Vielen“ in seinem Parmenides und anderen späten Dialogen stellt.²³

In einem gelungenen klassischen Gedicht, dessen Form sich an Goethes einfachem Mailied²⁴ sehr gut zeigen läßt, repräsentieren die Strophen eine Abfolge von Metaphern, die eine nach der anderen einer Auflösung zustreben. Die metaphorische Zuordnung jeder dieser Strophen entsteht durch Ironien, wobei einer Strophe weder eine einschränkende wörtliche noch eine symbolische Bedeutung zugeordnet werden darf. Die abschließende Metapher, insbesondere ihr letzter Doppelvers, verändert die metaphorische Zuordnung – d. h. die „Bedeutung“ – des Gedichts insgesamt radikal. Es ist diese abschließende, subsumierende Metapher, die die Idee des Gedichtes als Ganzem ausmacht.

Um ein solches Gedicht oder seine klassische Vertonung ganz zu erfassen, ist eine wiederholte Durchsicht des gesamten Gedichts erforderlich, bis der Punkt erreicht ist, wo zwei Bedingungen erfüllt sind: Erstens, daß die Idee des vollständigen Gedichts klar ist; zweitens, daß die Beziehung jedes Fortschritts innerhalb des Gedichts bis zum Erreichen des Schlußpunktes klar ist.²⁵ Ist dieses Erfordernis erfüllt, entsteht im Geist die Idee des gesamten Gedichts als Ergebnis einer Spannung zwischen zwei buchstäblich platonischen Gedankenqualitäten. Die erste ist die Idee des abgeschlossenen Gedichts in seiner Gesamtheit; diese Idee bleibt unverändert vom Beginn des erneuten Lesens der ersten Zeile bis zur momentanen Stille nach dem Lesen der letzten Zeile. Die zweite Idee ist die fortlaufende Metamorphose, die die Idee des Gedichts beim Fortschreiten vom Anfang bis zum Ende erfährt. Bei Platon nennt sich diese letzte Gedankenqualität das Werden. Die Spannung zwischen der festen Vorstellung, der Idee des abgeschlossenen Gedichts als Ganzem, und dem metamorphischen Prozeß des Werdens, durch den die vollendete Idee erreicht wird, ist die „Energie“ des Gedichts.

Die gleiche Anforderung muß an die Aufführung jeder klassischen musikalischen Komposition gestellt werden. Im einfachsten Fall ist sich der Künstler bei der musikalischen Aufführung darüber bewußt, die vollendete (vollständige) Komposition erreicht zu haben, wodurch eine Spannung entsteht, die Metamorphose in der Aufführung nachzuvollziehen – die Spannung zwischen der vollendeten Idee der Komposition und dem Augenblick ihrer Entwicklung während der Aufführung.

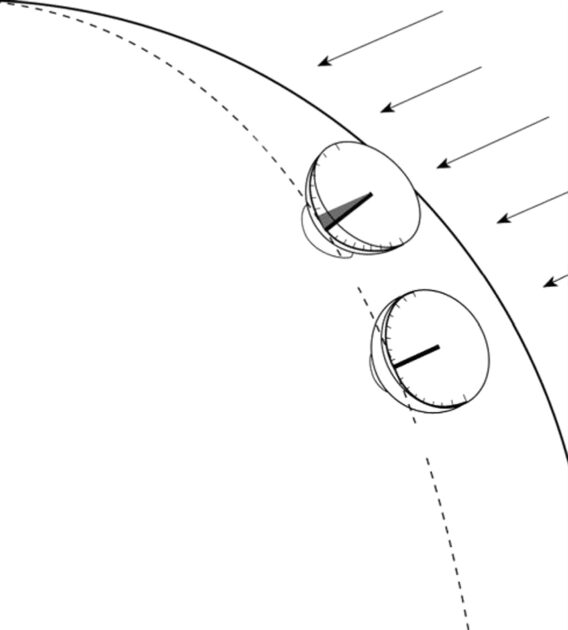
Das gleiche Prinzip beschreibt Eratosthenes‘ Berechnung der Erdkrümmung: Ein Entwicklungsprinzip wird offengelegt, indem die einander widersprechenden Ablesungen der einzelnen Sonnenuhren neu erlebt werden, um ein Veränderungsprinzip zu erzeugen, das sich mit dem Endergebnis deckt. Für Eratosthenes wird der Schlüssel zu dem Erzeugungsprinzip die Beziehung zwischen dem Umfang eines Kreises und einem Geradenbündel, das von einer momentan festen Position eines der Sonne entsprechenden Punktes zur Erde verläuft. Auf diese Weise gelangte Eratosthenes zu einer realistischen Berechnung des Erdumfangs – 2200 Jahre, bevor überhaupt jemand die Erdkrümmung gesehen hat.

Diese Beispiele aus der Poesie, der Musik und dem Wirken von Platons Athener Akademie sind sämtlich Beispiele platonischer Ideen, denen Riemann den Begriff Geistesmassen zuschrieb. In den Naturwissenschaften generell nehmen solche Ideen anfangs den vermeintlichen Charakter von Ideen an, die aus heftigen Widersprüchen zwischen Sinnesbeobachtungen entstehen, Widersprüchen, die der naiven Sinnesgewißheit und allgemein akzeptierten wissenschaftlichen Aussagen Hohn sprechen. Recht häufig tritt diese Verhöhnung auf grausam verheerende Weise auf. Diese Ideen, die das für dieses Paradox verantwortliche Erzeugungsprinzip benennen sollen und die durch entsprechende Meßmethoden bestätigt werden, repräsentieren gültige Entdeckungen physikalischer Prinzipien. Diese besonderen erwiesenen Prinzipien werden gemeinhin als platonische Ideen bezeichnet. Sämtliche gültigen Ideen der „Dimensionalität“ in einer n-fachen physikalischen Raumzeit-Mannigfaltigkeit haben diese Qualität einer platonischen Idee.

Alle solche Ideen haben somit die Form paradoxer Singularitäten im Verhältnis zu dem vorherigen mathematischen Referenzbereich. Der Charakter dieser Ideen als Singularitäten entsteht dadurch, wie ihre Entstehung subjektiv erzeugt wird: Durch die gleichen Prozesse, die dem Verstehen und der Komposition eines klassischen Strophengedichts zugrundeliegen. Die „Singularität“ und die damit verbundene mathematische Unstetigkeit entstehen durch die gegensätzlichen Zeitempfindungen, die mit der Wechselwirkung vollendeter Ideen mit dem Prozeß ihrer Entwicklung in Verbindung stehen.²⁶

Diese Metaphern lassen sich nicht aus der Mathematik oder anderen verwendeten Sprachformen ableiten. Innerhalb der Sprache selbst erscheinen sie lediglich in reflektierter Form von Singularitäten wie mathematischen Singularitäten oder anderen paradoxen Andeutungen, die sich im Sprachmedium widerspiegeln. Die ontologische Existenz der Singularität liegt außerhalb der Erzeugung der entsprechenden Markierung im Bereich der Sprache selbst.

Jedes Theorem, das die Existenz von Unstetigkeiten in der Mathematik zu leugnen meint, basiert somit auf einem tautologischen Trugschluß der Komposition, indem Konstruktionen verwendet werden, die axiomatisch von einer Linearisierung ausgehen, um die völlig irrelevante Frage zu beweisen, daß jede Konstruktion dieser Art außerstande ist, eine mathematische Existenz zuzuerkennen, die nicht linear ist!

Eine formale mathematische Unstetigkeit oder ein dichterisches Paradox ist lediglich die Markierung, die die Metapher als Fußabdruck auf das formal definierte Sprachmedium setzt. Die eigentliche Metapher, die sich in der angedeuteten Markierung oder dem Paradox reflektiert, existiert nur außerhalb des Mediums. Sie findet sich an drei Orten. Sie liegt erstens in der Substanz des Prozesses, den die Sprache zu beschreiben versucht. Sie liegt zweitens auch in den geistigen Prozessen des Wissenschaftlers oder Künstlers. Sie existiert drittens in den souveränen geistigen Prozessen jener im Publikum, die auf die Markierung der Singularität sokratisch reagieren, indem sie im eigenen Geist die Idee replizieren, die ihre Markierung auf dem Kommunikationsmedium hinterlassen hatte.

In der mathematischen Physik erfolgt die Bestätigung von Ideen, die solchen Markierungen entsprechen, gewöhnlich durch Messungen, die zeigen, daß diese Ideen mit einem Effekt übereinstimmen, der sich nicht mit den alten Ideen deckt, an deren Stelle die neuen Ideen treten sollen.

Dieser Umstand läßt sich sehr gut anhand eines Riemann-Papiers von 1860 mit dem Titel „Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite“ verdeutlichen.²⁷ Die Tatsache, daß eine Beschleunigung auf Geschwindigkeiten über der Schallgeschwindigkeit eine Singularität erzeugt, bedeutete für Riemann, daß es in diesem Bereich transsonische Phänomene gibt, die dann von Ludwig Prandtl und Adolf Busemann untersucht wurden. Dieses von Riemann entdeckte Prinzip führte durch die Mitwirkung eines deutschen Luftfahrtspezialisten nach dem Zweiten Weltkrieg zum ersten erfolgreichen Überschallflug eines amerikanischen Flugzeugs. Im Gegensatz dazu standen die gegenteilige falsche Auffassung durch Hermann Helmholtz, Lord Rayleigh und Theodor von Karman, die wiederholt Riemanns Arbeit attackiert hatten.²⁸

Nimmt man ein etwas typischeres Beispiel, wie das erwähnte Experiment von Eratosthenes, erreicht man die empirische Bestätigung einer solchen Singularität durch Messungen, die im Bereich arithmetischer Größen liegen. Dies ist jedoch nicht die einzige Grundform, um eine platonische Idee empirisch zu beweisen. Wie aus Riemanns erwähntem Papier über Stoßwellen hervorgeht, liefert uns auch eine nichtarithmetische Singularität, die eine präzise Mächtigkeit, aber keine arithmetische Größe hat, die mathematische Form des erforderlichen Beweises. Riemanns erfolgreiche Vorhersage von Phänomen, die nicht auf das angeführte Beispiel des Überschallflugs beschränkt war, sondern auch die isentropische Kompression bei der thermonuklearen Zündung betraf, ist hierfür ein Beispiel.

Leibniz‘ Universalsprache (characteristica universalis)

In Bezug auf die ontologischen Implikationen der Metapher selbst greift Riemann in den posthum erschienenen Schriften ein Thema auf, das zuvor von Leibniz behandelt und später vom Verfasser wieder aufgegriffen wurde. Man muß den Umstand berücksichtigen, daß platonische Ideen, die als gültige Prinzipienentdeckungen erkennbar sind, in jenen souveränen Geistesprozessen des Individuums erzeugt werden, die für symbolische Kommunikationsmedien wie die formale Mathematik unzugänglich sind. Doch trotz der überirdischen Qualität, die man fälschlich versucht ist, solchen Geistesprozessen beizumessen, führen solche Ideen dazu, daß die physische Macht des Menschen zunimmt, die Natur insgesamt zu beherrschen.

In dieser Hinsicht dienen diese Schriften Riemanns dazu, unseren Blick zurück auf Leibniz‘ Begriff einer characteristica universalis zu richten, der gewöhnlich unbelebte, lebende und kognitive Prozesse in unserem Universum in sich schließt. Mit diesem Themenbereich beschäftigt sich Riemann in den ersten beiden posthum erschienenen Papieren: „I. Zur Psychologie und Metaphysik“ und „II. Erkenntnistheoretisches“. Nach der Niederschrift dieser Papiere hat sich Riemann nirgendwo in seinen Veröffentlichungen mehr explizit zu diesen epistemologischen Grundlagen der Wissenschaft geäußert. Von 1854 an beschränkte er sich in seinen veröffentlichten Schriften hauptsächlich auf die mathematische Physik, mit einigen Vorstößen in die Biophysik,²⁹ obgleich er diese persönliche Sichtweise in mathematisch-physikalischen Fragen zweifellos nicht aufgegeben hat. Hierin liegt mit die besondere Bedeutung seiner posthum veröffentlichten Schriften, um die tieferen Implikationen seines Gesamtwerks zu verdeutlichen.

Meine eigenen Entdeckungen in der physikalischen Ökonomie gründen sich auf meine leidenschaftliche Beschäftigung mit Leibniz in der Jugendzeit und meine anschließende energische Verteidigung von Leibniz gegen die Angriffe Immanuel Kants auf ihn, was direkt mit Leibniz‘ Begriff einer characteristica universalis zu tun hat. Meine Entdeckungen wurden außerdem ausgelöst durch die positivistischen Exzesse von Norbert Wieners „Informationstheorie“ und der ähnlichen Inkompetenz in den systemanalytischen Arbeiten von Wieners Kollegen John von Neumann; diese positivistischen Verrenkungen habe ich als Parodien auf Kants Angriffe auf Leibniz behandelt. Aus diesem Grund verlieh meine erneute Lektüre Riemanns diesem Studium den gleichen Nachdruck auf Leibniz‘ characteristica universalis, den wir in den ersten zwei Schriften von Riemanns posthum erschienenen Schriften vorfinden.

Der Kern von Wieners Betrug mit der „Informationstheorie“ lag darin, daß er den Begriff „negative Entropie“ übernahm und mißbrauchte, der zuvor hauptsächlich dazu diente, den qualitativen Unterschied zwischen lebenden und unbelebten Prozessen zu bestimmen, wie sie sich auf makroskopischer Ebene zeigen.³⁰

In einer erfolgreichen modernen Realwirtschaft – meinem Forschungsgebiet – findet das biologische Erscheinungsbild der „negativen Entropie“ seinen Ausdruck in der Forderung, daß das Verhältnis der „freien Energie“ zur „Systemenergie“ nicht abnehmen darf, obgleich die Werte für Kapitalintensität und Energieintensität pro Kopf und pro Quadratkilometer gleichzeitig ansteigen müssen. Dieses gewünschte Ziel erreicht man gewöhnlich durch eine Steigerung der (physischen) Arbeitsproduktivkräfte, indem in den wissenschaftlichen und technologischen Fortschritt investiert wird.

Betrachten wir zusammenfassend das entsprechende Argument, das an anderer Stelle ausgeführt ist.³¹

In der physischen Ökonomie werden die Hauptphänomene der Wirtschaftsprozesse in Form von Warenkörben sowohl des notwendigen physischen Verbrauchs wie auch bestimmter wichtiger Dienstleistungsbereiche gekennzeichnet, (in der modernen Gesellschaft) beschränkt vor allem auf Erziehung, Gesundheitsversorgung und Wissenschaft und Technologie allgemein. Diese Warenkörbe definieren sich pro Kopf (der Arbeitskräfte), pro Haushalt und pro Quadratkilometer entsprechender Landfläche. Die Warenkörbe sind unterteilt in persönlichen Verbrauch, in Produktionsprozesse und in solche Verbesserungen der benutzten Landfläche, die man als „grundlegende wirtschaftliche Infrastruktur“ bezeichnet. In einer physischen Ökonomie muß eine funktionale Beziehung herrschen zwischen der Höhe der Warenkörbe und den Arbeitsproduktivkräften, die man nach Produktion und Konsumption des Inhalts dieser Warenkörbe bemißt.³²

Darin ist ein Differentialausdruck enthalten: Welcher Input (Verbrauch) ist erforderlich, um einen bestimmten Output notwendiger Produkte für den Konsum beizubehalten? Ohne noch die genaue Antwort auf diese Frage an jeder beliebigen Stelle zu kennen, ist die Idee hinter der Frage klar. Die Idee läßt sich am besten als Begriff der potentiellen relativen Bevölkerungsdichte ausdrücken.³³

Die Höhe des kombinierten Verbrauchs der Warenkörbe, die erforderlich ist, um mindestens eine konstante Rate der potentiellen relativen Bevölkerungsdichte aufrechtzuerhalten, wird neben die „Systemenergie“ gestellt. Der Output des Warenkorbinhalts über diese erforderliche Höhe hinaus wird neben die „freien Energie“ gestellt. Die „freie Energie“ gilt als „nicht verschwendet“, sofern sie in Form von Warenkörben zur Ausweitung des Wirtschaftsumfangs wie zur Steigerung der potentiellen relativen Bevölkerungsdichte konsumiert wird. In letzterem Fall muß die Kapitalintensität („Systemenergie“ pro Kopf, pro Haushalt und pro Quadratkilometer) ansteigen, und auch die Energiedichte muß zunehmen. Erforderlich dabei ist, daß das Verhältnis der „freien Energie“ zur „Systemenergie“ trotz eines steigenden Werts der „Systemenergie“ pro Kopf, pro Haushalt und pro Quadratkilometer nicht sinken darf.

Die Steigerung der potentiellen relativen Bevölkerungsdichte wird – unter der Voraussetzung, daß diese Vorgaben erfüllt sind – als wirtschaftliches Gegenstück für das, was sich in der Biologie als „negativ-entropische“ evolutionäre Selbstentwicklung der Biosphäre und in der Wissenschaftsdisziplin ausdrückt, die Wladimir I. Wernadskij als Biogeochemie bezeichnet hat. Um jede Verwirrung mit dem in der „Informationstheorie“ mißbrauchten Begriff „negative Entropie“ zu vermeiden, soll hier der Begriff „Nicht-Entropie“ verwendet werden.

In dem Bereich, den Wernadskij als Biogeochemie definiert, bedingt dies die Evolution der Biosphäre, um das ganze System auf einen höheren Organisationszustand zu heben; Wernadskij folgt dabei dem gleichen Gedankengang, den man auch an vielen anderen Stellen trifft, vor allem bei Leibniz‘ Begriff der characteristica universalis und auch in den erwähnten Abschnitten von Riemanns posthum veröffentlichten Schriften.

Wiener hat alles durcheinandergebracht, indem er darauf beharrte, daß „negative Entropie“, wofür er den Neologismus „Negentropie“ benutzte, lediglich eine Umkehr der durch Ludwig Boltzmanns H-Theorem beschriebenen statistischen Entropie sei. Wenn man im Gegensatz zu Wieners mechanistischen Mätzchen die Menschheit und deren Aktivitäten als Teil des Planetensystems begreift, bedeutet die wachsende Macht des Menschen über die Natur, wie sie sich in einer Zunahme der potentiellen relativen Bevölkerungsdichte³⁴ ausdrückt, in Wirklichkeit eine Steigerung der relativen „negativen Entropie“ oder „Nicht-Entropie“ des Planetensystems als Ganzem. Anders gesagt, die Entwicklung der Menschheit bewirkt in der Gesamtheit des Systems, mit dem die Menschheit interagiert, einen evolutionären Aufwärtsimpuls.

So gesehen, hat sich das menschliche Denken zwar im Bereich der Lebensprozesse entwickelt, doch die ökologischen Besonderheiten der menschlichen Gattung, die vollständig auf seine Erkenntnisfähigkeit zurückzuführen sind, trennt den Menschen von und erhebt ihn über alle anderen Lebewesen. Unser Universum umfaßt somit das Zusammenwirken drei voneinander unterscheidbaren Prozessen: das Unbelebte, das Lebende und das Kognitive. Das allgemein umfassende Prinzip, das in einem solchen Universum vorherrscht, ist Leibniz‘ Vorstellung einer characteristica universalis.

Nach der heutigen verbreiteten Schulmeinung wirft das eben Gesagte die Frage auf: „Ist es nicht notwendigerweise der Fall, daß eine steigende ,Nicht-Entropie‘ der Gesellschaft auf Kosten einer zunehmenden Entropie des Universums erfolgt, mit dem die Gesellschaft interagiert?“ Anders gesagt, ist die Beziehung der Gesellschaft zum übrigen Universum nicht das, was von Neumanns Verehrer ein „Nullsummenspiel“ nennen? Im Kern geht es um die Frage, ob die Idee einer „universellen Entropie“ nicht das Ergebnis wissenschaftlicher Entdeckungen ist, sondern der fahrlässigen Übertragung einer axiomatisch linearen, mechanistischen Weltsicht auf die Auslegung von Ergebnissen kinetischer Gasmodelle. Aus diesem Grund ergibt sich ein amüsanter Doppelsinn in der ironischen Bedeutung, die Norbert Wiener in seiner Arbeit dem Begriff „Gastheorie“ beilegt.

Der Widersinn beliebter Lehrversionen des „universellen Entropiegesetzes“ ergibt sich daraus, daß jede rationale Anstrengung, das Universum im Großen zu beschreiben, zu einem evolutionären Modell führt, in dem sich Entwicklung als Fortschreiten zu relativ höheren Organisationszuständen äußert. Mathematisch gesehen zeigt sich dieses Fortschreiten zu höheren Organisationszuständen im Entstehen physikalischer Systeme, deren Charakteristika sich nicht feststellen lassen, ohne sich einer Mathematik immer höherer Mächtigkeiten zu bedienen. Der Versuch, die effiziente Gerichtetheit solcher Entstehungsprozesse höherer Mächtigkeiten zu erklären, führt jeden Versuch ad absurdum, die Existenz von Materie im Sinne eines mechanistischen „Baustein“-Dogmas zu erklären. Es ist deutlich, daß erkennbar höhere physikalische Mächtigkeitszustände durch Transformationen des gesamten Systems erfolgen und nicht durch den Zuwachs von Objekten eines mechanistisch festgesetzten Bereichs.

Der Unterschied zwischen der (nicht-entropischen) Entwicklungsanschauung und den mechanistischen Sichtweisen wie bei Kant wird von Riemann in den ersten drei der erwähnten Schriften dargestellt. Wie bei Eulers absurder Attacke auf Leibniz‘ Monadologie 1761 steckt hinter der kantianischen mechanistischen Sichtweise, mit der sich Richard Clausius, Lord Kelvin und Hermann Grassmann ihren haltlosen „Zweiten Hauptsatz der Thermodynamik“³⁵ zusammenreimten, die Annahme einer „axiomatischen Linearisierung im Kleinen“. Man schaffe eine Mathematik, in der alles unter der axiomatischen Annahme gefaßt wird, daß alles im Universum mit dem Euklidischen Wunschdenken einer überall gültigen vollkommen linearen Ausdehnung übereinstimmt, und das bis ins extrem Große und ins extrem Kleine. Der wahre Gläubige betrachtet dann jede Formulierung, die mit einem solchen mathematischen „Beweis“ unvereinbar ist, als „unbewiesen“, und alles, was man für erforderlich hält, um die Widerspruchsfreiheit im Theoremgitter einer solchen Mathematik zu erhalten, betrachten alle blindgläubigen, ach so professoralen, kopfnickenden Dussel auf ihren internen Konferenzen für „bewiesen“.³⁶

Sobald man erkennt, daß eine solche Mathematik keinerlei Beweis für die hier vorliegenden Fragen darstellt, scheint das großzügigste Taktgefühl, das die Verfechter des „Zweiten Hauptsatzes“ für rationale Menschen aufbringen könnten, der berühmte schottische Urteilsspruch zu sein: „Nicht bewiesen.“ Kein Axiom der Mathematik wird durch ein formales mathematisches Theoremgitter bewiesen, das auf dieser Annahme basiert.

Mit diesen einschränkenden Beobachtungen wollen wir die anstehende Frage einordnen. Wenden wir uns deshalb direkt der Frage von Leibniz‘ characteristica universalis zu.

Sämtliche Steigerungen der potentiellen relativen Bevölkerungsdichte des Menschen – vom Menschenaffen mit einem Potential von mehreren Millionen bis zum menschlichen Potential von mehreren Milliarden heute – beruhen auf Veränderungen im produktiven Verhalten der Gesellschaft, vor allem auf der allgemeinen Anwendung der Früchte des wissenschaftlichen und technologischen Fortschritts.³⁷

Jede der überlieferten Entdeckungen ist bekannt, indem der ursprüngliche Entdeckungsakt im Geist des Zuhörers nachvollzogen wird. Sofern die Erziehung der Jugend nach diesem Grundsatz verläuft, besteht das heutige Wissen in einer Ansammlung all jener Singularitäten, die durch frühere Entdeckungen zum Nutzen der jetzigen Generationen übermittelt wurden: Genauso wie die Schüler heute wissenschaftliche Analphabeten wären, wenn sie nicht die ursprünglichen Entdeckungen von Mitgliedern der platonischen Akademie in Athen von Platon, Eudoxos und Theaitetos bis Eratosthenes auf diese Weise nacherleben würden. Ohne eine klassische Erziehung der Jugend in den großen klassischen Werken der Poesie, Tragödie, Musik und Naturwissenschaft bis zurück zu den Grundsteinen der modernen Zivilisation vor über 2500 Jahren kann es keine wirklich zivilisierte oder zumindest rationale Gesellschaft geben – eine grausame Wirklichkeit, die sich heute auf unseren Straßen und in unseren Regierungen und Universitäten so unerbittlich vollzieht.

In jeder derartigen gültigen Entdeckung steckt das Prinzip, das wir hier mit dem topologischen Symbol (n + 1)/n versehen haben. Jede Entdeckung ist eine Singularität dieser Art. Fortschritt im Wissen ist eine Ansammlung solcher Singularitäten. Wie Riemann in den posthum veröffentlichten Schriften hervorhebt, ist diese Ansammlung von Wissen ein sich gegenseitig beeinflussender Prozeß; jede neue Geistesmasse steht in Wechselwirkung mit allen anderen, die sich zuvor im Geist gebildet haben. Mit jedem Gedanken spiegelt sich diese Zunahme der Singularitäten effizient wider: mathematisch gesehen steigt die Dichte der Unstetigkeiten für jedes beliebig gewählte Intervall menschlichen Einwirkens an. Es ist diese Zunahme der „Dichte von Unstetigkeiten“, die die Form der „Nicht-Entropie“ und die Form des Wirkens charakterisiert, die „Nicht-Entropie“ z. B. in Form der Zunahme der potentiellen relativen Bevölkerungsdichte der Gesellschaft erzeugt.
Entscheidend ist, daß dieser so definierte Wissenszuwachs gleichbleibend effizient ist. Das Universum gehorcht dem Befehl der schöpferisch-geistigen Kräfte des Menschen! Wie es in Genesis 1 heißt, übt die Menschheit somit Herrschaft über die Natur aus. Umgekehrt ist das Universum offensichtlich so eingerichtet, daß es dafür empfänglich ist, sich der Autorität jener Macht schöpferischer Vernunft zu unterwerfen, die ein dem menschlichen Individuum eigenes Potential ist.

Durch das wiederholte Nachvollziehen der ursprünglichen gültigen Grundsatzentdeckungen, die die Anhäufung menschlichen Wissens bis zum heutigen Tag darstellen, sind wir in der Lage, die besonderen Merkmale dieser Form der schöpferischen Vernunft zu erkennen, mittels derer gemeinhin gültige Entdeckungen erzielt wurden. Diese Erfahrung kennen wir, wie Johannes Kepler, als Vernunft oder, wie Gottfried Leibniz, als notwendige und hinreichende Vernunft. Sobald wir erkennen, daß die Wissensanhäufung der Menschheit die Macht des menschlichen Willens darstellt, das Universum nach dem in ihm eingebetteten Gesetz zu beherrschen, haben wir uns bewiesen, daß die Vernunft, wie wir sie subjektiv auf diese Weise definieren, auch eine effiziente Annäherung an die Vernunft ist, wie sie scheinbar objektiv als effizientes Prinzip existiert, das das Universum als Ganzes durchdringt.

Was wir in Form von „Nicht-Entropie“, wie in der Zunahme der potentiellen relativen Bevölkerungsdichte der Gesellschaft, erkennen, ist das Merkmal der Vernunft, wie sie wirksam, „objektiv“, im Universum insgesamt, aber auch als Fähigkeit existiert, die Prinzipien der Vernunft „subjektiv“ durch die Wirksamkeit gültiger Prinzipienentdeckungen in Wissenschaft und Kunst anzuwenden.

Sobald man das erkennt, ist uns klar, daß das Universum im extrem Kleinen oder im extrem Großen nicht linearisiert ist. Es ist im extrem kleinen und extrem großen Bereich gleichermaßen „nicht-entropisch“. Um dies zu verdeutlichen, genügte es, den Schwerpunkt in Riemanns Beiträgen zur mathematischen Physik von der eng verstandenen Physik hin zur Sichtweise von Leibniz zu verlagern, zur Sichtweise der physikalischen Ökonomie, zur Sichtweise der wirksamen Verbindung zwischen gültiger menschlicher Vernunft und der wachsenden Macht des Menschen über das Universum. So können wir sagen, daß die Nicht-Entropie, wie sie sich in Riemanns topologischem Ausdruck (n + 1)/n widerspiegelt, dem entspricht, was Leibniz als characteristica universalis bezeichnete.

1. Der deutsche Originaltext findet sich in Bernhard Riemanns gesammelte mathematische Werke und wissenschaftlicher Nachlass. Hrgs. Heinrich Weber, Leipzig: Druck und Verlag von B.G. Teubner, 1876–1902. Im weiteren als Riemanns Werke bezeichnet. Darin insbesondere „Fragmente philosophischen Inhalts“, S. 475–506.[↩]
2. Siehe Bernhard Riemann, „Über die Hypothesen, welche der Geometrie zu Grunde liegen“, Werke, S. 254–269. Dies ist Riemanns berühmte Habilitationsschrift vom 10. Juni 1854, auf die sich Albert Einstein berief, als er Riemanns Werk als eine Grundlage der Allgemeinen Relativitätstheorie bezeichnete. Zur Datierung der in der Habilitationsschrift enthaltenen Erkenntnisse, siehe auch Heinrich Webers Verweis auf eine Anmerkung Riemanns, die die in seine Arbeit eingeflossene Entdeckung auf den 1. März 1853 datiert. Werke, S. 502.[↩]
3. Zu Eulers Angriff auf Leibniz siehe Lyndon H. LaRouche jr. „Christentum und Wirtschaft, Die wissenschaftlichen Grundlagen einer neuen, gerechten Weltwirtschaftsordnung“, Dr. Böttiger Verlags-GmbH, Wiesbaden, 1992, Siehe auch Eulers „Briefe an eine deutsche Prinzessin“ (von ihm auf den 5. Mai 1761 datiert), worin er zum zweiten Mal ausdrücklich Leibniz angreift. Sein erster Angriff erfolgte im Rahmen des Skandals um Pierre-Louis Maupertius, dessen Betrug in der Frage des „Prinzips der geringsten Wirkung“ aufgedeckt wurde und 1753 zu seiner Entlassung als Präsident der Berliner Akademie führte. Euler war der Hauptkomplize von Maupertius bei dessen Betrug. Es seien hier die ursprüngliche Übereinstimmung zwischen Riemann und Weierstrass betont, nicht ihre zweitrangigen methodischen Unterschiede.[↩]
4. Siehe den Briefwechsel zwischen Leibniz und Clarke über die Beziehung zwischen unendlichen Reihen und dem Diffentialkalkül (Der Leibniz-Clarke Briefwechsel, Volkmar Schüller, hrgs., Akademie Verlag, 1991.) Leibniz‘ Ausarbeitung des Diffentialkalküls beginnt zwar bereits in früheren Tätigkeiten, aber archivarisch läßt sich nachweisen, daß das, was später als Leibnizscher Diffentialkalkül bekannt wurde, zwischen 1672 und 1676 in Paris an Jean-Baptiste Colberts Königlicher Akademie der Wissenschaften ausgearbeitet wurde. Leibniz‘ erste Schrift, worin er seine Entdeckung darstellt, wurde in Paris 1676, unmittelbar vor seiner Rückkehr nach Deutschland, zur Veröffentlichung eingereicht. Isaac Newtons internationales Ansehen und die Newton-Clarkeschen Angriffe auf Leibniz sind das Werk des in Paris lebenden venezianischen Abtes Antonio Conti (1677–1749), der in ganz Europa ein Geflecht von Salons betrieb, dessen Hauptaufgabe es war, Leibniz zu diskreditieren und Newtons Reputation zu begründen. Dr. Samuel Clarke war ein Agent Contis, genauso wie die Berliner Kreise um Maupertuis und Euler.[↩]
5. „Es führt dies hinüber in das Gebiet einer andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur der heutigen Veranlassung nicht zu betreten erlaubt,“ Werke, S. 268.[↩]
6. Siehe Lyndon H. LaRouche jr., „Why Most Nobel Prize Economists Are Quacks,” Executive Intelligence Review, 28. Juli 1995, und Lyndon H. LaRouche jr., “Non-Newtonian Mathematics for Economists,” Executive Intelligence Review,. 11. Aug, 1995.[↩]
7. Siehe “How Eratosthenes Measured the Unseen” (Figure 2), in Lyndon H. LaRouche jr., “Kenneth Arrow Runs Out of Ideas, But Not Words,” 21st Century, Fall 1995, pp. 34–53, und auch Lyndon H. LaRouche jr., „Wissenschaft ist nicht Statistik“, FUSION, Jg. 40, Nr. 2, 2019, S. 41, Abbildung 1.[↩]
8. Dieses Bild ist eine genaue Darstellung von Platons Beschreibung der Schatten, welche die Realität auf die menschliche Wahrnehmung wirft, als seien diese Schatten der Widerschein vor Vorgängen, die sich auf der Wand einer im Inneren von einem Feuer erleuchteten Höhle darstellen.[↩]
9. Greek Mathematical Works, Ivor Thomas, trans., 2 vols. (Cambridge, Mass.: Harvard University Press, 1980), Vol. II, p. 273, note c.[↩]
10. Christian Huygens, Abhandlung über das Licht, Wissenschaftliche Buchgesellschaft Darmstadt, 1964.[↩]
11. Das „Brachistochronenproblem“ von Johann Bernoulli (1696) oder die Äquivalenz der kürzesten Zeit und der geringsten Wirkung.[↩]
12. Damit lassen sich die Annahmen einiger verbreiteter Begriffe der Differentialgeometrie nicht rechtfertigen. Der Grund für dieses warnende Wort wird weiter unten noch deutlich.[↩]
13. Formell läuft Eulers Aussage auf eine Rechtfertigung der völlig willkürlichen Behauptung hinaus, daß lineare Ausdehnung nach naiver Euklidischer Vorstellung unbegrenzt vollkommen stetig sei. Da Eulers angeblicher Beweis dieser Aussage auf der Behauptung jenes Axioms beruht, das es zu beweisen vorgibt, beweist Eulers Tautologie überhaupt nichts. Eulers Kindereien in dieser Frage pflanzten sich über Lagrange und Laplace auf Cauchys Verballhornung von Gottfried Wilhelm Leibniz‘ Version des Kalkulus fort.[↩]
14. Die Angriffe auf Planck kamen zunächst aus deutschen Wissenschaftskreisen zur Zeit des Ersten Weltkriegs und setzten sich dann in der Zeit der berühmten Solvay-Konferenzen der 1920er Jahre mit den Rasereien von Niels Bohr und anderen Komplizen Bertrand Russells fort.[↩]
15. Das ist im wahrsten Sinne eine uralte Frage. Diese topologische Aufgabe ist das gleiche ontologische Paradox zwischen dem „Einen“ und dem „Vielen“, das sich in Platons Parmenides-Dialog stellt.[↩]
16. D. h. was Euler mit Hilfe seiner ziemlich einfältigen Tautologie bei seinem Angriff auf Leibniz 1761 verteidigt, ist die naive, Euklidische Grundannahme einer vollkommenen Linearisierung, die sich unendlich bis ins sehr Große und sehr Kleine fortsetzt.[↩]
17. „Das Wort Hypothese hat jetzt eine etwas andere Bedeutung als bei Newton. Man pflegt jetzt unter Hypothese alles zu Erscheinungen Hinzugedachte zu verstehen.” Riemann, Werke, S. 493[↩]
18. Das Problem hierbei ist, daß viele verbildete Leser mit höheren Abschlüssen im Kunstbereich die gleiche Schwierigkeit im Umgang mit dem Begriff „Metapher“ haben, wie radikale Positivisten sie mit dem Begriff „mathematische Unstetigkeit“ erleben. Anfang des 17. Jahrhunderts haben Empiristen wie Thomas Hobbes eine abscheuliche, tatkräftige und anhaltende Kampagne geführt, um Metaphern und den Konjunktiv aus dem englischen Sprachgebrauch zu verbannen. Das jüngste Wiederaufleben dieser radikalexistentialistischen Dekadenz – auch als „Dekonstruktivismus“ von Prof. Jacques Derrida u. a. bekannt – ist der Auswuchs einer jahrhundertelangen Kampagne von Empiristen, logischen Positivisten und anderen linguistischen Experten, den Ursprung der Schriftsprache, selbst der klassischen Poesie, im „Text“ als solchen und nicht in der ironiereichen Sprache zu lokalisieren.[↩]
19. Im sehr Kleinen vergleicht man Unstetigkeiten mit Blick auf ihre mathematische Kardinalität, nicht als arithmetische Werte. Unter Bezugnahme auf Georg Cantor wird dieser Unterschied hier durch den Begriff „transinfinitesimal klein“ bezeichnet.[↩]
20. Mozart schuf mit dem 1785 vertonten Goethe-Gedicht Das Veilchen die Gattung des deutschsprachigen Kunstliedes und benutzte dabei die neue Kompositionsmethode der „Motivführung“. Siehe Handbuch von Stimmung und Register, Schiller-Institut (Hrsg.), Dr. Böttiger Verlag, 1996, S. 199–228.[↩]
21. Ebenda, S. 220 f. Besonders hier der Verweis auf Gustav Jenner, Johannes Brahms als Mensch, Lehrer und Künstler: Studien und Erlebnisse, Verlag Walter Wollenweber, Gräfelfing bei München, 1989. Jenners Bericht, wie Brahms ihn anwies, ein Gedicht zu einem Strophenlied zu vertonen, hat direkte Bedeutung zu der oben im Text entwickelten Frage.[↩]
22. Siehe Lyndon H. LaRouche jr., „Musical Memory and Thorough-Composition“, Executive Intelligence Review, 1. September 1995, S. 50–63. auf deutsch erschienen als „Die Grundlagen der Motivführung“, Ibykus, Nr. 56, 3. Quartal 1996, S. 45–58.[↩]
23. Platons Dialog Parmenides muß als eine Art einleitende Schrift für alle seine späten Dialoge verstanden werden. Darin spricht er die Herausforderung, das ontologische Paradox, an, das in verschiedenen Aspekten Gegenstand aller seiner anderen späten Dialoge ist.[↩]
24. LaRouche, „Die Grundlagen der Motivführung,“ a. a. O., nach der Zwischenüberschrift „Dichtung, Malerei und Wissenschaft“, S. 48.[↩]
25. Siehe Jenners Darstellung der Empfehlung von Brahms an ihn, „ein Gedicht vor der Komposition lange im Kopf mit mir herumzutragen.“ Siehe Anmerkung 21.[↩]
26. Die entsprechenden Topologiebegriffe leiten sich aus dieser Überlegung ab.[↩]
27. Riemann, Werke, S. 145. Uwe Henke und Steve Bardwell besorgten eine englische Übersetzung dieses Textes, der im von der Fusion Energy Foundation herausgegebenen International Journal of Fusion Energy, Vol. 2, Nr. 3, 1980, S. 1–23, erschienen ist.[↩]
28. Die Veröffentlichung dieser Übersetzung durch die Fusion Energy Foundation (FEF) hat eine eigene interessante Geschichte. Mitte bis Ende der 1970er Jahre hatte sich die FEF mit ihren wichtigen Arbeiten zur Förderung der Kernfusion mit Trägheitseinschluß einen Namen gemacht. In Folge davon wurden zwei Vertreter der FEF, Charles B. Stevens und Dr. Steven Bardwell, in die Sowjetunion eingeladen, um an einer internationalen Wissenschaftskonferenz über Trägheitseinschluß teilzunehmen. Vor ihrer Abreise trafen sich die beiden FEF-Vertreter mit LaRouche und anderen an einem Ort in der Bronx, um von LaRouche eine Anforderungsliste für ihren Moskaubesuch zu erhalten. LaRouche verlangte, daß sie sowjetische Wissenschaftler nach nicht klassifizierten Dokumenten fragten, die zeigten, wie Riemanns Arbeiten über isentropische Kompression in die ursprüngliche Entwicklung der thermonuklearen Zündung Einzug fanden. Sie erhielten derartige nicht klassifizierten Dokumente, worin Riemanns Fortpflanzungs-Papier in diesem Zusammenhang genannt wurde. Auf einem späteren Treffen im gleichen Jahr, auf dem Stevens und Bardwell über die Moskauer Konferenz Bericht erstatteten, betonte LaRouche, daß das gleiche Papier auch auf Modelle der realwirtschaftlichen Entwicklung angewendet werden könnte und unterbreitete eine Reihe von Ungleichheiten für die höchst erfolgreichen vierteljährlichen US-Wirtschaftsprognosen, die das Nachrichtenmagazin Executive Intelligence Review (EIR) zwischen 1980 und 1983 herausgab.[↩]
29. Siehe vor allem seine nachdrücklich bestätigte Analyse in der Schrift Mechanik des Ohres, Riemann, Werke, S. 316–328, nachgedruckt in FUSION 03/1984, S. 29–34.[↩]
30. Wie schon wiederholt an anderer Stelle bemerkt, findet es der Autor wünschenswert, die gesamte Naturwissenschaft in vier funktional unterschiedliche Forschungsbereiche aufzuteilen. Die Astrophysik und Mikrophysik sind zwei Bereiche, die entweder zu groß oder zu klein sind, um direkt mit den Sinnen erfaßt zu werden. In einem dritten Bereich, der Biophysik, behandeln wir den grundlegenden Unterschied zwischen Prozessen, wie etwa organischen Verbindungen, die in einem Fall als Teil eines Lebensprozesses fungieren und in einem anderen Fall wiederum nicht. Das entzieht sich auch der einfachen Sinneswahrnehmung. Neben diesen drei Bereichen bleibt der Bereich der Makrophysik übrig, in dem Sinneswahrnehmungen eine größere unmittelbar Rolle spielen.[↩]
31. Lyndon H. LaRouche jr., „Why Most Nobel Prize Economists Are Quacks,” und Lyndon H. LaRouche jr., “Non-Newtonian Mathematics for Economists”. Siehe Anmerkung 6.[↩]
32. Die Begründung für den Verbrauch privater Haushalte lieferte Gottfried Wilhelm Leibniz in „Societät und Wirtschaft“ (1671), LSB IV, 3, S. 866-883. Siehe auch https://www.hs-augsburg.de/~harsch/germanica/Chronologie/17Jh/Leibniz/lei_soci.html[↩]
33. Zur „potentiellen relativen Bevölkerungsdichte“ siehe Lyndon H. LaRouche jr., „Was Sie schon immer über Wirtschaft wissen wollten!“, Böttiger-Verlag, 1985. Dieses einführende Lehrbuch ist neben dem englischen Original in zahlreichen Sprachen erschienen, so in deutsch, russisch, ukrainisch und jüngst auch in armenisch.[↩]
34. Pro Kopf der Arbeitskraft, pro Haushalt und pro Quadratkilometer der verwendeten Landfläche.[↩]
35. Kelvin war es, der Clausius diese radikal-mechanistische Interpretation von Sadi Carnots Arbeit nahebrachte. Hierbei und wie bei allen seinen Angriffen auf Bernhard Riemann stützte sich Clausius bei mathematischen Fragen seines Unternehmens auf Hermann Grassmann. Siehe Riemann, Werke, Anmerkung auf S. 257. Die entscheidende Rolle, die das Axiom der Linearisierung im Kleinen in Grassmanns Arbeiten spielte, insbesondere bei allen seinen Schriften über den „Zweiten Hauptsatz“ und seinen Angriffen auf Riemann, drückt sich in seiner berühmten Arbeit von 1844 aus, mit der er einen einschlägigen Zweig der modernen Vektoranalyse, die sogenannte Ausdehnungslehre, begründete.[↩]
36. Der ehemalige FEF-Vorsitzende Morris Levitt hat 1978 ein von J. Clerk Maxwell verfaßtes Dokument ausgegraben, das damals in der FEF für viel Heiterkeit sorgte. In diesem Dokument antwortete Maxwell auf eine Frage, warum er Persönlichkeiten wie Wilhelm Weber und Bernhard Riemann (und insbesondere auch dem Begründer der Elektrodynamik, Ampère) kaum eine der Entdeckungen zuschrieb, die Maxwell stillschweigend als Arbeiten von Michael Faraday oder von sich selbst präsentierte. In Maxwells Antwort hieß es ganz offen, daß „wir“ (gemeint waren die Kreise um Kelvin u. a.) beschlossen hätten, alle Arbeiten zu übergehen, die auf einer Geometrie beruhten, die „nicht die unsrige“ sei. Ähnlich äußert sich Maxwell in seinem Hauptwerk. Lord Rayleighs Verriß von Riemanns Fortpflanzungs-Papier läuft auf das gleiche hinaus: Die mechanistische Weltsicht, die die empiristische britische Anschauung von ihrem Altmeister Paolo Sarpi übernommen hat, läuft immer auf die Behauptung einer überall geltenden perkussiven Kausalität in einem Universum hinaus, das auch im sehr Kleinen axiomatisch linearisiert ist.[↩]
37. Der Fortschritt im menschlichen Dasein ist nicht nur auf den wissenschaftlichen und technologischen Fortschritt zurückzuführen. Metaphern, die aus der klassischen Poesie, Tragödie und Musik entstanden sind, spielen in der wachsenden Existenzfähigkeit der Menschheit eine ebenso entscheidende Rolle wie das, was man üblicherweise „Naturwissenschaften“ nennt. Gleichwohl bedeuten gültige grundlegende wissenschaftliche Entdeckungen, wie bereits erwähnt, den allgemeineren Fall für sämtliche Ausdrucksformen der schöpferischen menschlichen Geisteskräfte als Metapher, wie es der große englische Dichter Percy Shelley in seiner Schrift „Verteidigung der Poesie“ dargestellt hat: Eine „gesteigerte Kraft, tiefe und glühende Ideen über den Menschen und die Natur mitzuteilen und zu empfangen.“ Was hier oben geäußert wurde, sollte so verstanden werden, daß wissenschaftliche Ideen für Metaphern allgemein stehen.[↩]