Lyndon LaRouche äußert sich in diesem Aufsatz, der auf Englisch in EIR, Jg. 10, Nr. 39 vom 11. Oktober 1983 erschien, zu der Denkweise von Biologen, die aufhören sollten, Leben lediglich als „Nicht-Tot-Sein“ zu betrachten. Dazu ist es erforderlich, daß wichtige Veränderungen im gegenwärtigen wissenschaftlichen Denken erfolgen.
Ich habe kürzlich in einer Schrift mit einem Vorschlag zum medizinischen Zivilschutz angeregt, ein allgemeines, internationales Forschungsprotokoll einzurichten, das sich mit allen Erkrankungen im Zusammenhang mit Gewebealterung und damit zusammenhängenden Fragen beschäftigt. Der Grund dafür ist, daß Mediziner, die in der Forschung und damit zusammenhängenden präventivmedizinischen Aktivitäten beschäftigt sind, überwiegend ein Reservoir professioneller Fähigkeiten darstellen, auf das notfalls vorübergehend zurückgegriffen werden kann, ohne dabei die Kontinuität ihrer längerfristigen, primären Funktionen zu beeinträchtigen.

Was das Forschungsprotokoll selbst anbelangt, so war es meine Aufgabe, an dieser Stelle die Funktionen und Auswirkungen solcher Forschungsprogramme vom Standpunkt der Wirtschaftswissenschaft darzulegen. Im Gegensatz zu den Ansichten bestimmter Versicherungsstatistiker, die es lieber sähen, daß Menschen im Rentenalter beim ersten Anzeichen einer Krankheit schnell – vorzugsweise in nicht näher definierter Würde – sterben, ist die Erhöhung der Lebenserwartung ein unverzichtbares Ergebnis des wirtschaftlichen Fortschritts, und wenn Menschen im sogenannten Rentenalter ihre Funktionsfähigkeit behalten, können sie auf verschiedene Weise direkt und indirekt weiter zur nationalen Produktivität beitragen.
In der Wirtschaftswissenschaft befassen wir uns nicht nur mit den Beiträgen der Technologie zur Steigerung der durchschnittlichen Produktivkraft der Arbeit, sondern auch mit der Tatsache, daß die Investition der Gesellschaft in die Bildung und die allgemeine Erfahrung eines Menschen um so länger rentabel ist, je länger er lebt. Man könnte dies als das „Präsident-Charles-de-Gaulle“- oder „Bundeskanzler-Konrad-Adenauer“-Prinzip der politischen Ökonomie bezeichnen.
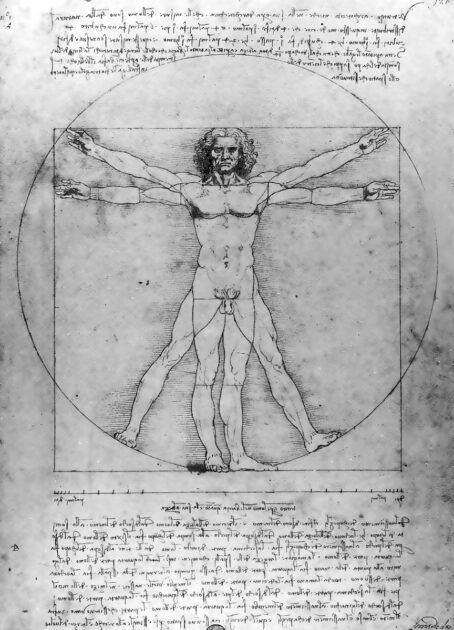
Die Wirtschaftswissenschaft hat auch direkte Bedeutung für einige Funktionen der medizinischen Forschung. Seit den Arbeiten von Luca Pacioli und Leonardo da Vinci am Ende des 15. Jahrhunderts wissen wir, daß sich lebende Prozesse in elementarer und einzigartiger Weise von nicht-lebenden Prozessen unterscheiden. Alle lebenden Prozesse zeichnen sich in ihren morphologischen Wachstums- und Funktionsmerkmalen durch eine harmonische Charakteristik aus, die man den Goldenen Schnitt nennt. Das Prinzip dahinter ist auch das Grundprinzip wirtschaftlicher Prozesse; dies mag für die Ohren des Laien beim ersten Hören eine verblüffende Information sein, aber nach kurzem Nachdenken verfliegt die Skepsis in diesem Punkt.
Die Gesellschaft ist ein Organismus, der sich durch die für den Menschen spezifischen Tätigkeiten auszeichnet, und die Wirtschaft begann mit der Entwicklung der landwirtschaftlichen Revolution. Es sollte daher nicht verwundern, daß das durchgängige Prinzip, das erfolgreiche von gescheiterten Volkswirtschaften unterscheidet, ein Spiegelbild desselben Prinzips ist, das lebende von nicht-lebenden Prozessen unterscheidet.
Der besondere Aspekt des wirtschaftlichen Fortschritts, der diesen Zusammenhang unmittelbar zum Ausdruck bringt, ist die Definition von Technik, wie ihn Gottfried Wilhelm Leibniz vor etwa 300 Jahren erstmals formuliert hat. Durch die grundlegenden Entdeckungen von Carl Friedrich Gauß zu Beginn des 19. Jahrhunderts und durch die Arbeiten von Gauß‘ berühmtem Nachfolger Bernhard Riemann erschließt sich der Zusammenhang zwischen dem Grundprinzip des technischen Fortschritts und dem zentralen Prinzip des Lebens sehr genau. Dieser Zusammenhang hat unmittelbare Auswirkungen auf bestimmte elementare Aspekte der Forschung, wie z. B. die Alterung von lebendem Gewebe und Krankheiten wie Krebs, die in diese allgemeine Forschungskategorie fallen.
Im Zusammenhang mit dem oben erwähnten Papier, worin ich diese Bemerkungen über das Prinzip des Lebens gemacht habe, sind eine Reihe von Fachleuten und anderen Personen an mich herangetreten und haben mich um eine Klärung und weitere Ausarbeitung dieses Punktes gebeten. Ich wiederhole meine Äußerungen an dieser Stelle und beginne mit den allgemeinen Hintergründen, um darin die entscheidende Frage anzusiedeln.
Die Bedeutung des Goldenen Schnitts
Die Wiederentdeckung dessen, was heute als isoperimetrisches Theorem der Topologie bekannt ist, durch Kardinal Nikolaus von Kues im 15. Jahrhundert war nicht nur das zentrale Element von Kues‘ Werk, das die moderne europäische Wissenschaft begründete, sondern setzte auch unter Kues‘ Nachfolgern ein strenges physikalisches Denken in Gang. Diese Wiederentdeckung war unabdingbar für das genaue Verständnis des Inhalts von Platons Timaios-Dialog, von dessen Umsetzung die Gesamtheit der grundlegenden Beiträge der modernen europäischen mathematischen Wissenschaft abhing.
Die drei zentralen Elemente dieses Timaios-Dialogs sind erstens das isoperimetrische Prinzip, zweitens der Beweis, daß nur fünf Arten regelmäßiger Polyeder im sichtbaren Raum konstruiert werden können, und drittens ein Prinzip, das von Platon als Hypothese der höheren Hypothese bezeichnet wurde. Das formale Problem, mit dem sich die europäische Wissenschaft bei dem Versuch konfrontiert sah, den Inhalt des Timaios zu verstehen, bestand bis zu Cusas Arbeit darin, daß das isoperimetrische Prinzip im Timaios nur implizit angesprochen wurde und daß die Europäer von der irrigen Ansicht ausgingen, daß Platons Prinzipien der Geometrie mit der syllogistischen Grundstruktur der Lesart von Euklids Elementen übereinstimmten, die mehr als ein Jahrhundert nach Platon in Ägypten aufgeschrieben wurden.
Cusas Wiederentdeckung des isoperimetrischen Prinzips führte zur Ausarbeitung einer nichteuklidischen Geometrie der Art, wie sie von Prof. Jakob Steiner im 19. Jahrhundert entwickelt wurde, einer synthetischen Geometrie ohne Axiome oder syllogistische Strukturen, die allein auf dem Konstruktionsprinzip basiert und nur vom isoperimetrischen Prinzip ausgeht.
Es sei hier hervorgehoben, daß sich gegen Ende des 16. Jahrhunderts in England und anderswo unter dem Einfluß von Francis Bacon, Galileo Galilei, René Descartes, Robert Fludd und anderen eine Schule der mathematischen Physik entwickelt hat, die im Gegensatz zu den Arbeiten von Cusa, da Vinci, Kepler und anderen steht. Diese gegenteilige Schule stützte sich weiterhin auf axiomatisch-syllogistische Strukturen wie die der ägyptischen Versionen von Euklids Elementen, wobei der Schwerpunkt zunehmend auf dem vermeintlichen Primat solcher axiomatisch-syllogistischer Strukturen lag, d. h. weniger auf der Geometrie als auf einfacher Arithmetik.
Die Principia Mathematica von Russell-Whitehead, der moderne logische Positivismus und die sogenannte neue Mathematik, die etwa Ende der 1950er Jahre in den Schulen eingeführt wurde, sind radikale Versionen dieses axiomatisch-syllogistischen Systems. Daß sich diese radikal-positivistische Strömung an den Universitäten und unter den Fachleuten vor allem seit Mitte des 19. Jahrhunderts und insbesondere seit dem Versailler Vertrag durchgesetzt hat, führte dazu, daß die strengen Prinzipien, die den grundlegenden Entdeckungen der europäischen physikalischen Wissenschaften zugrunde liegen, selbst unter sonst begabten Fachleuten nicht mehr bekannt sind.
Die Besonderheit meiner eigenen wirtschaftswissenschaftlichen Tätigkeit besteht darin, daß die ursprünglichen Entdeckungen, die ich 1952 gemacht habe, unmittelbar auf den Arbeiten Bernhard Riemanns, des großen Nachfolgers von Carl Friedrich Gauß, beruhten. Um meine eigenen wirtschaftswissenschaftlichen Entdeckungen weiterzuentwickeln, war es notwendig, daß meine Mitarbeiter und ich den Fortschritt der europäischen Wissenschaft von den Anfängen bei Cusa über Kepler, Leibniz, Euler, die École polytechnique, Gauß usw. rekonstruieren mußten, wobei wir uns sowohl auf nicht beachtete Primärmanuskripte in Archiven als auch auf veröffentlichtes Primärmaterial führender Wissenschaftler der Zeit von Cusa bis Riemann, Weierstraß und Cantor im 19. Jahrhundert bezogen. Dabei mußten wir einen Großteil des ausgefeilten, syllogistischen Überbaus der modernen mathematischen Physik eliminieren und die methodischen und ontologischen Grundannahmen, die der heutigen wissenschaftlichen Forschung zugrunde liegen, neu untersuchen.
In der heutigen Situation sind sich Wissenschaftler nicht bewußt, daß ein großer Teil des Überbaus der heutigen mathematischen Physik auf Grundannahmen beruht, die sich bei ihrer Einführung empirisch als falsch, ja sogar als absurd und willkürlich erwiesen haben, angefangen mit den völlig falschen Annahmen, die von Bacon, Fludd, Galilei, Descartes u. a. aufgebracht wurden. Fachleute wie auch Laien sind sich heute nicht bewußt, in welchem Maße Aussagen zu wissenschaftlichen Themen nicht das Ergebnis empirischer Untersuchungen der Natur sind, sondern Produkte von Methoden, die der Beschreibung der Natur übergestülpt werden, Methoden, die auf nachweislich falschen Grundannahmen beruhen. Unter normalen Umständen erscheint der fehlerhafte mathematische Apparat der modernen Wissenschaft beispielsweise in den Ingenieurwissenschaften nicht als fehlerhaft. Der mathematische Apparat erscheint adäquat, solange die Anwendung in der Praxis nicht in Bereiche vordringt, in denen ontologische Grundannahmen eine wichtige Rolle für die vorliegende Aufgabe spielen.
Wenn ich oder andere bestimmte Aussagen zu grundlegenden Fragen machen, sei es in der Wirtschaftswissenschaft oder in anderen Bereichen, ist die erste Reaktion selbst unter begabten Fachleuten nicht nur Ungläubigkeit, sondern auch Wut. Die erste Reaktion ist die Behauptung, die allgemein anerkannten Methoden der mathematischen Physik scheinen doch sehr gut zu funktionieren, so daß diese Methoden in keiner Hinsicht als verdächtig anzusehen seien. Doch wie wir an mehreren Stellen gezeigt haben, ist an unserer Kritik nichts Absurdes, geschweige denn etwas Falsches, wenn der Fachmann seine Aufmerksamkeit nur von den heutigen Lehrbüchern auf die Primärschriften und veröffentlichten Quellen lenken würde, die von den führenden Denkern des wissenschaftlichen Fortschritts im Laufe der letzten 500 Jahre des Aufstiegs der europäischen Wissenschaft beigetragen wurden.
Der Unterschied zwischen diesen zwei gegensätzlichen methodischen Strömungen in der modernen europäischen Wissenschaft hat die tiefgreifendsten praktischen Auswirkungen, wenn wir uns auf das Bemühen konzentrieren, eine strenge ontologische Definition des Lebens zu erstellen. Wie das Beispiel „Informationstheorie“ von Wiener und Shannon unterstreicht, basieren die Methoden zur Definition von Lebensprozessen heute axiomatisch entweder auf der statistischen Mechanik oder auf gegensätzlichen, mystischen Doktrinen, die dem Bergsonschen Vitalismus ähneln. Wie ich noch zeigen werde, war bereits vor den Arbeiten von Descartes bewiesen worden, daß die Phänomene des Lebens anders definiert werden müssen. Die empirische Grundlage, die zuerst von Pacioli und da Vinci und später von Kepler erarbeitet wurde, hatte diesen Beweis erbracht. Die Beiträge von Leibniz, die grundlegenden Entdeckungen von Gauß und die Arbeiten von Riemann lieferten die strengen Mittel für eine erneute, tiefgründigere Herangehensweise an die empirischen Fragen, die zuvor von da Vinci und Kepler behandelt worden waren.
Damit ist das kontroverse Element beschrieben, über das ich jetzt berichte.
Ein Zeitgenosse und Mitarbeiter Platons, der am Tempel des Ammon in Kyrenaika arbeitete, hatte bewiesen, daß in der Geometrie des sichtbaren Raums nur fünf Arten von regelmäßigen Polyedern konstruiert werden können. Wie Pacioli auf der Grundlage von Cusa zeigte und wie Leonhard Euler später einen neuen, strengeren Beweis erbrachte, haben alle fünf Körper eine einzigartige, funktionale Verbindung, so daß vier von ihnen aus der Konstruktion eines einzigen abgeleitet sind, nämlich des 12-seitigen Dodekaeders, dessen 12 Seiten jeweils gleiche, regelmäßige Fünfecke sind. Bei dieser Konstruktion tritt die Harmonie des Goldenen Schnitts nicht nur bei der Konstruktion des Fünfecks aus dem isoperimetrisch definierten Kreis auf; derselbe Goldene Schnitt charakterisiert auch die Konstruktion des Dodekaeders selbst.
Meine Mitarbeiter und ich haben Keplers Behandlung dieses Prinzips in seiner Ableitung, die sich als die einzig gültige Ableitung der astronomischen Gesetze unseres Universums erwiesen hat, eine wichtige Korrektur hinzugefügt. Wir haben bewiesen, daß die richtigen Gesetze auf einem harmonischen System beruhen, das mit der wohltemperierten musikalischen Polyphonie von Bischof Zarlino und Johannes Sebastian Bach übereinstimmt. Mit anderen Worten, die Prinzipien von Bachs wohltemperiertem System der Polyphonie existierten tatsächlich als fundamentale Gesetze des Universums, bevor es den ersten Musiker gab.
Die Bedeutung dieser Korrektur läßt sich wie folgt zusammenfassen, insofern sie für den in dieser Abhandlung behandelten Punkt relevant ist.
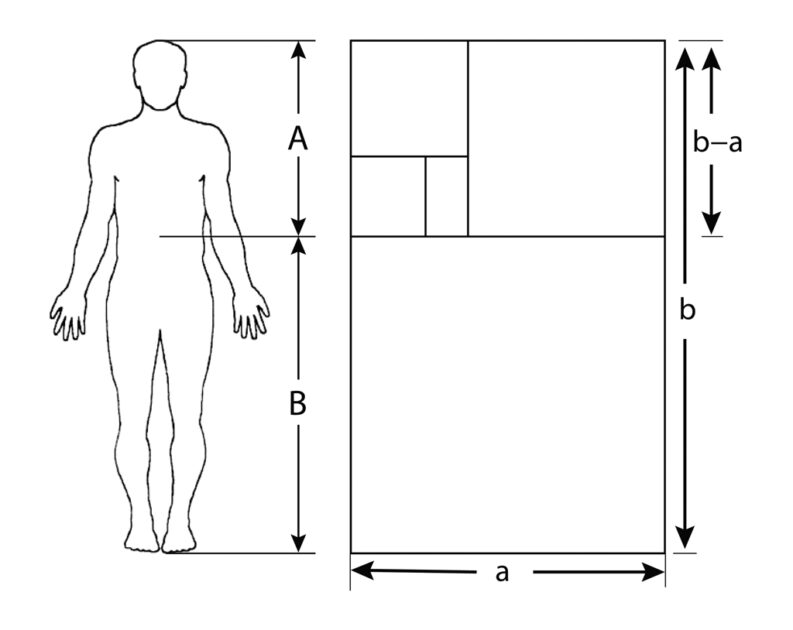
In erster Näherung besteht die Bedeutung des Goldenen Schnitts für die mathematische Physik auf unserem Planeten darin, daß er nur als charakteristisches Prinzip der Morphologie lebender Prozesse erscheint. Dies scheint sich zum Teil zu erklären, wenn wir den Goldenen Schnitt mit der sogenannten Fibonacci-Reihe vergleichen. Die Fibonacci-Reihe ist eine idealisierte Darstellung des einfachen Bevölkerungswachstums. Wenn die Fibonacci-Reihe fortschreitet, konvergieren ihre harmonischen Eigenschaften mit denen des Goldenen Schnitts. An dieser Konvergenz ist nichts Mystisches; eine einfache geometrische Konstruktion der Fibonacci-Reihe zeigt, warum eine solche Konvergenz notwendigerweise auftreten muß. Betrachtet man das Wachstum von Zellpopulationen oder jede ähnliche Art biologischer Aktivität von diesem Standpunkt aus, verschwinden alle Geheimnisse.
Berücksichtigt man unsere eigene Korrektur der Keplerschen Harmonik, ergibt sich sofort eine noch tiefere Einsicht.
Die Tatsache ist hier entscheidend, daß Keplers astronomische Gesetze – mit zwei Einschränkungen – eindeutig richtig sind. Die Unzulänglichkeit der Keplerschen Gesetze besteht darin, daß sie wohltemperierte Harmonien statt einfacher diatonischer Harmonien verwenden sollten, und daß sie in ihrer gegebenen Form für die Behandlung relativistischer Phänomene ungeeignet sind. Ansonsten sind sie gültig, denn sie werden sowohl aus dem isoperimetrischen Prinzip als auch aus dem Prinzip der fünf platonischen Körper abgeleitet. Das heißt, das Grundprinzip, das den Keplerschen Gesetzen und dem daraus abgeleiteten Prinzip der Schwerkraft zugrunde liegt, ist der Goldene Schnitt – derselbe Goldene Schnitt, von dem Pacioli, da Vinci und Kepler versicherten, daß er für lebende Prozesse im Gegensatz zu nichtlebenden Prozessen charakteristisch sei. Mit anderen Worten: Die Gesetze der Astronomie zeigen, daß das Universum als Ganzes von demselben Prinzip beherrscht wird, das sonst für lebende Prozesse charakteristisch ist. In heutiger Sprache ausgedrückt, sind die grundlegenden Gesetze unseres Universums die eines universell negentropischen Prozesses.
Was bedeutet diese astronomische Tatsache wirklich? Die Antwort war bereits in Platons Werk enthalten, doch in der mathematischen Physik wurde die Bedeutung dieser Antwort erst mit den grundlegenden Entdeckungen von Gauß und später Riemann richtig verstanden.
Schon Platon erkannte und betonte, daß das Universum, wie wir es sehen, nicht genau das reale Universum ist. Heute würden wir sagen, daß unser geistiger Wahrnehmungsapparat so organisiert ist, daß unser Verstand das Bild des Universums auf gesetzmäßige, aber konsistente Weise verzerrt. Die Aufgabe der Wissenschaft besteht zuallererst darin, die Prinzipien dieser gesetzmäßigen, konsistenten Verzerrung herauszufinden und mit Hilfe dieser Entdeckung strenge, empirische Methoden zu entwickeln, um ein entsprechendes Bild des Universums jenseits dieser Verzerrung zu erhalten.
Der Beweis für Platons Argument ist die Demonstration, daß bestimmte geometrische Formen, die im sichtbaren Raum existieren, nicht im sichtbaren Raum konstruiert werden können. Ein Beispiel hierfür ist das regelmäßige siebenseitige Vieleck, das Heptagon. Dieses kann nur durch Hilfsfiguren konstruiert werden, die Mittel zur Konstruktion transzendenter Funktionen sind. Mit anderen Worten: Das reale Universum – im Unterschied zu den verzerrten Bildern dieses Universums, die unser geistiger Wahrnehmungsapparat erfaßt – beruht auf Prinzipien, die dem zugrunde liegen, was wir transzendentale Funktionen nennen.
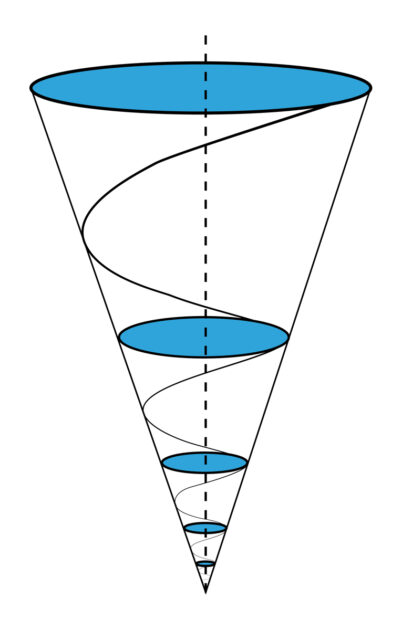
Alle transzendentalen Funktionen lassen sich auf ihre elementarste Form reduzieren, nämlich auf eine sogenannte selbstähnliche Spirale auf der Außenfläche eines Kegels oder auf der Außenfläche eines Zylinders. In der Wirtschaftswissenschaft stellt die selbstähnliche Spirale auf der Außenfläche eines Kegels Arbeit dar, und auf der Außenfläche eines Zylinders von unbestimmter Länge ist sie die Normalform kohärenter Strahlungsenergie.
Im Falle der selbstähnlichen Spirale auf der Außenfläche eines Kegels, der sogenannten logarithmischen Spirale, ergibt die Projektion dieser Spirale auf die kreisförmige Basis des Kegels eine ebene Spirale, deren charakteristischen Merkmale der Goldene Schnitt ist. Betrachtet man das als Projektion eines Dodekaeders auf die Ebene, wird die kreisförmige Basis des Kegels in 12 gleiche Sektoren geteilt, wodurch die Arme der Spirale in Segmente unterteilt werden, deren harmonische Längenverhältnisse denen des wohltemperierten Systems der Polyphonie entsprechen. Das Intervall der Quinte, das Intervall, das dem Goldenen Schnitt entspricht, definiert durch ein Ergänzungssystem alle harmonischen Beziehungen des wohltemperierten Systems der Polyphonie.
Die wesentliche Bedeutung dieser Beziehung wurde von Gauß in seiner Lösung des allgemeinen Begriffs elliptischer Funktionen entdeckt, eine Lösung, die sich aus seiner Bestimmung des sogenannten arithmetisch-geometrischen Mittels ableitet. Diese Lösung beruht auf den prinzipiellen Eigenschaften einer selbstähnlichen Spirale, die auf einem Kegel oder einer Ableitung einer konischen Funktion erzeugt wird. Dies bedeutet, um es kurz zu machen, daß die Gesetze des Universums auf der Tatsache beruhen, daß das reale Universum, das wir nur in seiner gesetzmäßig verzerrten Form als das sichtbare Universum sehen, von dem Grundprinzip der geringsten Wirkung beherrscht wird, in dem die geringste Wirkung der Arbeit in Form einer selbstähnlichen spiralförmigen Kegelwirkung auftritt, und daß das, was wir als Merkmale des Verhaltens im sichtbaren Raum sehen, Projektionen des realen Universums höherer Ordnung auf die Auffassungskraft unseres geistigen Wahrnehmungsapparats niederer Ordnung sind. Wie der Apostel Paulus sagt: „Jetzt sehen wir nur ein undeutliches Bild wie in einem trüben Spiegel“.
Um auf die unmittelbar vorliegende Frage zurückzukommen: Die Tatsache, daß lebende Prozesse in der Morphologie von Wachstum und Funktion das Merkmal des Goldenen Schnitts aufweisen, spiegelt also lediglich die Tatsache wider, daß im realen Universum die Ursache für dieses Ergebnis eine Wirkung ist, die dem Prinzip der geringsten Wirkung innerhalb des komplexen Bereichs entspricht.
Daraus folgt, daß man bei der Untersuchung der physikalischen Prinzipien lebender Prozesse das empirische Untersuchungsmaterial anders wählen muß, d. h. nicht in Materieteilchen, die sich innerhalb einer kartesischen Mannigfaltigkeit definieren, sondern man muß spezifische physikalische Transformationen lebender Prozesse wählen, die die Merkmale negentropischer Transformation in einer Riemann-Gauß-Mannigfaltigkeit aufweisen. In diesem Sinne müssen wir mit einem richtigen Verständnis der mathematischen Physik von Bernhard Riemann nicht nur an die Messung der charakteristischen Merkmale lebender Prozesse herangehen, sondern auch an die Wahl der empirischen Gegenstände.
Mit anderen Worten: Die statistische Mechanik muß aus der Biologie verbannt werden.
Es gibt drei Aspekte von Riemanns Arbeit, die sich auf diese Art Untersuchung am deutlichsten auswirken. Erstens, Riemanns Definitionen einer neuen Methode der mathematischen Physik, die er 1854 in seiner Habilitationsschrift Über die Hypothesen, die der Geometrie zugrunde liegen vorstellte. Zweitens Riemanns Betrachtungsweise der Elektrodynamik, mit Schwerpunkt auf seinen Begriff des retardierten Potentials. Drittens, Riemanns Anwendung des Prinzips des elektrodynamischen retardierten Potentials auf die Erzeugung akustischer Stoßwellen in seinem 1859 erschienenen Aufsatz Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite.

In dieser Arbeit greift Riemann das bereits von Leonardo da Vinci entwickelte Konzept der Hydrodynamik auf, wonach die Ausbreitung von Schallwellen in der Luft in einer Form erfolgt, die wir heute als Sinuswelle bezeichnen würden, und nicht durch das Aneinanderstoßen von Luftmolekülen. Riemann behandelt derartige Sinuswellen als selbstähnliche Spiralwellen auf der Außenfläche eines Zylinders von unbestimmter Länge. Er betrachtet die Schallwelle als eine solche selbstähnliche, spiralförmige Zylinderwelle und nimmt an, daß solche Wellen elektrodynamisch und nicht molekular-perkussiv sind. Damit sich diese Welle durch die Atmosphäre ausbreiten kann, muß sie die Atmosphäre für ihre Ausbreitung transparent machen.
In der Laserphysik nennt man dies heute induzierte Transparenz des Mediums. Diese Selbsttransparenz erfordert eine bestimmte Konfiguration der Luftmoleküle. Diese Konfiguration kann sich nicht schneller ausbreiten, als es die durchschnittliche Bewegung der Luftmoleküle erlaubt. Dies ist ein Beispiel von retardierter Ausbreitung des elektrodynamischen Potentials. Wenn dann die Luftmoleküle mit einem Kolben oder einer anderen Vorrichtung über diese Geschwindigkeit hinaus beschleunigt werden, übersteigt die Ausbreitungsgeschwindigkeit der Schallwellen die Grenzbedingung des verzögerten Ausbreitungspotentials in der Luft. Dies erzeugt einen einzigartigen Zustand, den wir als Stoßwelle kennen.

Wenn Riemanns Vorstellung von Stoßwellen richtig sei, so argumentierte Lord Rayleigh mit Nachdruck, müsse die gesamte statistische Mechanik in ihren Grundannahmen umgestoßen werden. Unter dieser Voraussetzung erklärte Rayleigh die Arbeit von Riemann aus dem Jahr 1859 für absurd. Später bewiesen dann die deutschen Physiker Ludwig Prandtl und Adolf Busemann, daß Riemann Recht hatte und Rayleighs Argumentation absurd war. Erwin Schrödinger stützte sich bei seiner berühmten Arbeit über die Natur des Elektrons ebenfalls auf Riemann, und das gleiche Prinzip bildet heute die Grundlage für das Prinzip der isentropischen Kompression in der Plasmaphysik. Riemanns Vorstellungen haben sich in dieser Frage wiederholt als richtig erwiesen, doch die von Rayleigh vertretenen verheerenden Folgen für die statistische Mechanik sind bis heute nicht ausreichend beachtet worden.
Betrachtet man die Riemannsche Methode als Ganzes, so muß man z. B. in der Biologie zu dem gleichen Ansatz kommen, den meine Mitarbeiter und ich für die Wirtschaftswissenschaften erfolgreich nachgewiesen haben. Bei allen experimentellen Arbeiten, die sich mit grundlegenden Fragen befassen, darf sich der experimentelle Ansatz nicht auf das vermeintlich selbstevidente besondere „Ding“, wie einzelne Moleküle, Gene usw., konzentrieren, sondern als primäre empirische Daten müssen nur solche Transformationen im Prozeß behandelt werden, die einer Phasenverschiebung in der Charakteristik des Gesamtprozesses entsprechen. Solche Transformationen müssen im Sinne eines singulären Merkmals der Transformation definiert werden. Transformationen, die eine solche Singularität beinhalten, müssen als ontologisch primäre Daten behandelt werden.
Dies ist insbesondere für lebende Prozesse erforderlich. Wir müssen aufhören, lebende Prozesse mit Methoden zu untersuchen, die für tote Dinge geeignet sind; wir müssen aufhören, Leben als etwas Nicht-Totes zu definieren, als etwas, das sich den statistischen Gesetzen toter Dinge widersetzt. Der Begriff „negative Entropie“ ist aus diesem Grund sehr unglücklich. Das Universum wird als axiomatisch entropisch angesehen – obwohl Kepler bereits schlüssig bewiesen hat, daß diese Annahme falsch ist – und es wird ein axiomatisch-syllogistischer mathematischer Apparat entwickelt, der auf der Annahme beruht, daß das Universum in erster Linie ein totes Etwas ist, dessen Zeitrichtung angeblich durch die Entropie vorbestimmt ist. Dann wird versucht, lebende Prozesse durch eine Mathematik des Todes zu definieren. Eine solche Mathematik, die naturgemäß die Kausalität aus den konstruierten Gleichungen ausschließt, zwingt uns dazu, die empirischen Daten lebender Prozesse so zu definieren, als ob sie primär aus toten Dingen zusammengesetzt sind.
Mit Vorstellungen lebender Prozesse, die sich aus solchen mathematischen Ansätzen und Versuchsanordnungen ableiten, wird Leben als Tod bewertet. Nicht lebende Prozesse führen die Untersuchung zu solchen Schlußfolgerungen; die Schlußfolgerungen stammen nicht von lebenden Prozessen, sondern vom Tod, der axiomatisch in die Mathematik eingebettet ist, die der Anordnung und Beschreibung der Experimente überlagert ist.
Der primäre Bezugspunkt, an dem sich biologische Experimente orientieren sollten, ist das Leben. Leben ist mathematisch definiert als jene Formen von Arbeit, die Materie durch eine singuläre Transformation auf einen höheren Organisationszustand heben. Solche Daten sind die nicht reduzierbaren experimentellen Daten der Biologie.
Einige weitere Bemerkungen helfen, dies verständlicher zu machen.
Leben und Mathematik
Um Leben zu verstehen, ist es unerläßlich, eine Mathematik zu entwickeln, die das Prinzip des Lebens widerspiegeln kann. Mit anderen Worten, wir müssen in der Lage sein, geometrische Bilder zu konstruieren, die als Spiegelbilder der Lebensprozesse betrachtet topologisch kongruent mit den lebenden Eigenschaften dieser Prozesse sind. Um dies zu erreichen, müssen wir ein Prinzip des menschlichen Geisteslebens isolieren, das seiner Natur nach mit der negentropischen Eigenschaft lebendiger Prozesse kongruent ist.
Das Problem, die Aufgabe, besteht hier nicht darin, das Verhalten von Lebensprozessen statistisch zu messen. Norbert Wiener et al. hatten in dieser Frage absurde Vorstellungen. Wieners Art, Mathematik zu betreiben, wurde nicht einmal vom großen Hilbert in Göttingen geduldet, berichtet EIR-Redakteur Uwe Parpart-Henke von seinen Forschungen, ganz zu schweigen von den Problemen, eine Mathematik zu definieren, die dem Verständnis lebender Prozesse angemessen ist. Die Aufgabe ist, ein geistiges Bild von Lebensprozessen zu konstruieren, ein geistiges Bild – eine Vorstellung – vom Wirkprinzip von Lebensprozessen. Es muß ein praktisches Konzept sein, das durch die Art seiner Konstruktion und Anwendung unsere Bemühungen auf nützliche Operationen ausrichtet, durch die die gewünschten Phasenverschiebungen innerhalb der Selbstentwicklung lebender Prozesse gesteuert werden können.
Diese Aufgabe ist das zentrale Thema der Wirtschaftswissenschaft. Auch ein wirtschaftswissenschaftlicher Laie mit einer allgemeinen wissenschaftlichen Berufsausbildung kann diesen Aspekt des Gegenstandes ohne weiteres erfassen.
Das allgemeine Maß für die wirtschaftliche Leistung von Gesellschaften ist die Zunahme der potentiellen relativen Bevölkerungsdichte, wobei die Bevölkerungsdichte die Zahl der Personen mißt, die die Aktivitäten dieser Gesellschaft pro durchschnittlichem Quadratkilometer bewohnbarer Fläche erhalten. Dieser Anstieg korreliert weitgehend und notwendigerweise mit dem Anstieg der Anzahl der pro Kopf eingesetzten Kilowattstunden-Äquivalente an nutzbarer Energie. In den Begriffen der elementaren Chemie bedeutet dies eine Zunahme der „Reduktionskraft“ einer Gesellschaft pro Kopf.
Gottfried Wilhelm Leibniz hat diesen Aspekt wirtschaftlicher Prozesse genau behandelt, als er die allgemeinen Prinzipien von Wärmekraftmaschinen aufstellte. In erster Näherung läßt sich sagen, daß die relative Arbeitsproduktivkraft zunimmt, wenn die von der Maschine genutzten Kilowattstunden Energie ansteigen. Wie Leibniz als erster betonte, gibt es jedoch eine entscheidende Anomalie, die zu berücksichtigen ist. Diese Anomalie läßt sich daran veranschaulichen, daß zwei Maschinen zwar dieselbe Menge an Kohle pro Stunde verbrauchen, es dem Arbeiter aber ermöglichen, die gleiche Art nützlicher Arbeit in unterschiedlichem Tempo zu verrichten. Diese unterschiedliche Organisation innerhalb einer Maschine ist die Leibnizsche Definition von Technik.
Der so gefundene und definierte geometrisch-physikalische Gehalt der Technik ist in erster Näherung das physikalische Korrelat des isoperimetrischen Prinzips, das Leibniz als das Prinzip der geringsten Wirkung definiert. Der technische Inhalt von Maschinen läßt sich durch den Maschinenzyklus definieren, der zwei Grundmerkmale hat. Das erste ist die Rotationswirkung, d. h. die geordnete durch die Rotation bewirkte Richtungsänderung der von der Maschine übertragenen Arbeit. Das zweite Merkmal ist die Erhöhung der Energieflußdichte des Arbeitsvorgangs, so daß die Maschine mehr Energie pro Quadratmeter aufgewendeter Leistung für die Produktion des Arbeitsergebnisses liefert, als durch die Energie repräsentiert wird, die die Maschine als Ganzes antreibt – ihre Input-Energie. Die Kombination dieser beiden Merkmale nimmt die Form kegelförmiger Rotation an, im Gegensatz zur einfacheren, kreisförmigen Rotation.
Die elementarsten Merkmale dieser Beziehung lassen sich wie folgt beschreiben.
Gegeben sei eine einfache selbstähnliche kegelförmige Spirale (eine elementare geometrische Aussage einer komplexen Variablen). Man betrachte zwei aufeinander folgende Zyklen dieser Spirale (zwei aufeinander folgende Drehungen der Spirale um den Kegel). Man betrachte die kreisförmigen Querschnitte des Kegels zu Beginn der beiden Zyklen und am Ende jedes der beiden Zyklen. Mögen die kreisförmigen Flächen die Energieflußdichte bestimmen. (Es ist sinnvoll, sich einen Laser vorzustellen, der eine Eingangsenergie von vielen Kilowatt pro Quadratmeter auf Anwendungsbereiche von beispielsweise nur 10-8 Quadratmetern konzentriert.) In diesem Fall sind wir vor allem an den Umständen interessiert, unter denen die ursprüngliche Energiezufuhr, die bei relativ niedrigen Energiestromdichten auf das Ziel einwirkt, keine Zustandsänderung des Zielsystems bewirkt, die konzentriertere Energiezufuhr jedoch eine solche Phasenverschiebung bewirkt. Solche Phasenverschiebungen sind paradigmatisch für unseren Begriff der Arbeit.
In dieser Konfiguration hat die elementare komplexe Variable, die die Erzeugung der Spirale definiert, die Spirale als ihr erstes Integral und das Volumen, das durch den Zyklus einer solchen Spirale begrenzt wird, als das definitive Integral der Spiralwirkung selbst. Darüber hinaus sind die Eigenschaften des Volumens Gaußscher Art: die iterative elliptische Teilung des Volumens entsprechend der arithmetisch-geometrischen Mittelwert-Beziehung sowie das Volumen und die Verschiebungen, die mit der kleinsten dieser iterativen Unterteilungen verbunden sind. Dieser kleinste Wert wird als äquivalent zu Leibniz‘ Definition der kleinsten Teilung behandelt, die dem „Delta“ der Differentialrechnung entspricht, und ist auch ontologisch kongruent mit dem Begriff des Wirkungsquantums.
Wir reduzieren alle Begriffe von Arbeit auf diese ontologische Form. Wir betrachten dann die Arbeit zur Erzeugung von Energie, wobei Energie normalerweise als der von einem kohärenten gerichteten Strahl abgestrahlten Energie definiert wird: die monochromatische zylindrische selbstähnliche Spiralform. Wir betrachten dann die durch die Anwendung dieser Energie geleistete Arbeit als Arbeit. Der Vergleich der Arbeit, die bei der Erzeugung von Energie anfällt, mit der Arbeit, die durch ihren Einsatz entsteht, ist die elementare Definition von Arbeit für den Einzelfall in wirtschaftlichen Prozessen.
Ein solcher Ansatz ist in Riemanns Habilitationsschrift von 1854 implizit enthalten. Angesichts des Prinzips der geringsten Wirkung als selbstähnliche konische Spiralwirkung definiert das so durch die Wirkung dieses Prinzips auf sich selbst universell entwickelte (elaborierte) Universum ein Universum der Ordnung N, so daß die hier definierte effektive Arbeit einen neuen Zustand des Universums, N + 1, erzeugt. Diese Beziehung bedeutet, daß die Wirkung auf das Universum in gewisser Weise durch die Ordnung des Universums N begrenzt ist.
Damit definiert sich implizit eine Grenze für die Teilung der hinzugefügten Wirkung, eine Grenze, die als Grenze für die iterative elliptische Teilung des Volumens eines Intervalls der zyklischen Wirkung ausgedrückt wird: das Wirkungsquantum. Der Wechsel von der Ordnung N zur Ordnung N + 1 dieses Universums bzw. des betrachteten Phasenraums von der Ordnung N zu N + 1 ist also mit einer Änderung der metrischen (Quanten-)Eigenschaften dieses Bereichs verbunden. Es sind diese Veränderungen der metrischen Wirkeigenschaften im Phasenraum, die die Substanz des empirischen Maßes der bewirkten Transformation, die Substanz der Arbeit, sind.
Im Falle wirtschaftlicher Prozesse (Gesellschaften) spiegelt sich diese metrische Veränderung in einer Zunahme der potentiellen relativen Bevölkerungsdichte wider. Die einzige Form der von der Gesellschaft geleisteten Arbeit ist die Vergrößerung dieses Potentials. Die einzige Arbeit, die in einer Gesellschaft geleistet wird, ist eine Tätigkeit, die funktionell effizient zu einer solchen Steigerung des Potentials der Gesellschaft als Ganzes beiträgt.
Diese Veränderungen, diese Arbeit, werden mit Hilfe willentlicher Fortschritte der Technologie erreicht.
Die Frage, die sich stellt, lautet daher: Was ist die Art des Handelns, durch das Gesellschaften den technischen Fortschritt hervorbringen? Diese Frage lenkt unsere Aufmerksamkeit auf die Hauptmerkmale des mathematischen Apparats, der für das Verständnis von Lebensprozessen erforderlich ist. Was ist das einsichtige Prinzip kreativer wissenschaftlicher Entdeckungen?
Die erforderliche Antwort erhalten wir, wenn wir Platons Begriff der Hypothese der höheren Hypothese untersuchen. Wir fassen diesen Begriff hier so einfach wie möglich zusammen. Aus dieser Sicht läßt sich der Geisteszustand, der dem schöpferischen Geistesleben entspricht, mehr oder weniger genau identifizieren. Diese Merkmale des schöpferischen Geisteslebens genügen wiederum den Erfordernissen einer Form der Mathematik, die für das Verständnis des Lebens geeignet ist.
Es gibt drei mögliche Stufen des geistigen Lebens, da das geistige Leben durch den Begriff der Hypothese definiert werden kann.

Einfache Hypothese: Auf der untersten Ebene des rationalen Geisteslebens versucht man, ein Problem mit Hilfe der Annahme zu verstehen, daß die vorherrschende Meinung im Großen und Ganzen richtig ist. Man versucht, ein Problem zu definieren, das glaubwürdig und für die allgemeine Meinung akzeptabel ist. Dies wird manchmal als „fremdbestimmtes“ Denken bezeichnet, d. h. als Geisteszustand, der sich auf solche Gedanken beschränkt, von denen man annimmt, daß die sprichwörtlichen Nachbarn, der Freundeskreis oder die herrschenden Autoritäten sie billigen. Bei wissenschaftlicher Arbeit ist der entsprechende Kreis die einschlägige Fachmeinung, die vorherrschenden Annahmen in der Wissenschaft im allgemeinen oder auch die Annahmen, die für besondere Aspekte der beruflichen Arbeit zutreffen.
Personen, die sich in diesem Geisteszustand befinden, werden niemals etwas entdecken, das für den Fortschritt des Wissens im allgemeinen von Nutzen ist.
Höhere Hypothese: Hierbei lehnt der Denker die „Andersgerichtetheit“ der einfachen Hypothese ab und versucht bei seinen Untersuchungen, bestimmte vorherrschende Annahmen aufzudecken und umzustoßen. Der kreative Denker ist von Natur aus eine Art Bilderstürmer, ein Mensch mit polemischer Geisteshaltung gegenüber den vorherrschenden wissenschaftlichen und anderen Annahmen seiner Zeit. Er ist „innenorientiert“ und vertraut auf seine Fähigkeit, empirisch und schlüssig zu beweisen, daß selbst die maßgebliche Meinung seiner Zeit in einem oder mehreren Punkten bsurd sein könnte.
Die höhere Hypothese ist offen gegenüber empirischen Belegen, um beweisen zu können, daß bestimmte vorherrschende Grundannahmen seiner Zeit umgestoßen werden müssen. Im Falle seines Erfolgs kommt es zu einer mehr oder weniger großen wissenschaftlichen Revolution – oder etwas Entsprechendem. Das gesamte Gebäude des mathematischen Wissens, das auf den fehlerhaften Annahmen beruhte, stürzt ein, und ein neues Gebäude muß auf der Grundlage der vorgenommenen Korrektur errichtet werden.
Das Kriterium dafür, ob solche Entdeckungen gültig sind oder nicht, zeigt sich letztlich in einer impliziten Zunahme der potentiellen relativen Bevölkerungsdichte der Gesellschaft: Führt die Entdeckung zu einer Zunahme der Macht des Menschen über die Natur als Ganzes oder nicht?
Hypothese der höheren Hypothese: Die Tatsache, daß die erfolgreiche Anwendung des Prinzips der höheren Hypothese zu einer Zunahme der potentiellen relativen Bevölkerungsdichte führt, impliziert, daß eine Abfolge derartiger wissenschaftlichen Revolutionen einen geordneten Charakter hat, und daß somit die dafür verantwortliche höhere Hypothese ebenfalls einen geordneten Charakter hat. Die Frage des empirischen Nachweises eines solchen Ordnungsprinzips ist ebenfalls Gegenstand einer Hypothese – der Hypothese eines allgemeinen Begriffs der höheren Hypothese.
Eine solche Hypothese der höheren Hypothese ist, mit anderen Worten, ein Prinzip der geordneten Abfolge schöpferischer wissenschaftlicher Entdeckungen. Sie muß nicht und kann vielleicht auch nicht perfekt sein, aber ihre Beherrschung im Laufe des menschlichen Fortschritts beschreibt einen zunehmender Vervollkommnungsprozeß.
In dieser letztgenannten Tätigkeit – der Formulierung der Hypothese der höheren Hypothese – liegt die wahre wissenschaftliche Kreativität des Menschen. Vom Standpunkt des bewußten Erfassens dieser Tätigkeit ergibt sich implizit eine Mathematik, mit der sich Lebensprozesse begreifbar machen lassen.
Die korrigierte Sichtweise der platonischen Hypothese von Platon, Augustinus, Dante Alighieri, Cusa, Pacioli, Kepler, Leibniz und anderen, wie sie zu einem großen Teil durch die Arbeiten von Gauß und Riemann erreicht wurde, liefert uns den notwendigen praktischen Bezugspunkt für die Arbeit von heute. Riemanns Habilitationsschrift von 1854 hat diese exemplarische Bedeutung und Tragweite.
Ein diskretes Objekt, das im falschen Naturbild der kartesischen Mannigfaltigkeit als selbstevident gilt, wird für uns zu einer relativen Erscheinung in einem kontinuierlichen Prozeß, der für uns in Bezug auf die Hypothese der höheren Hypothese steht. Zeit, Raum und Materie verlieren für uns ihren naiven selbstevidenten Charakter als sensorische Daten, und nur die Selbstentfaltung von Prozessen, die die relativistische Interdependenz aller drei als determinierte Aspekte eines kontinuierlichen Prozesses adäquat in sich schließt, hat noch eine Autorität für wissenschaftliche Arbeit. Die Wirklichkeit, die Wahrheit, liegt für uns im „Dazwischen“ jener Transformationen, die relativistische Phasenverschiebungen in Prozessen definieren.
Auf diese Weise stellen wir uns darauf ein, uns qualitativ von der naiven, hedonistischen Sichtweise abzukehren. Wir betrachten diskrete Sinnesobjekte nicht mehr als nicht reduzierbare, selbstevidente Dinge, sondern definieren die nicht reduzierbare, substantielle Form der Realität als die Verbform von „erschaffen“, „in Existenz bringen“. Nur negentropische Transformationen in Prozessen stellen die Substantialität des Universums, die Substantialität der stetigen Mannigfaltigkeit, des komplexen Bereichs der stetigen Mannigfaltigkeit dar.
Der jüdisch-christliche Standpunkt in der Wissenschaft
In Westeuropa war der wissenschaftliche Fortschritt etwa vom 4. Jahrhundert v. Chr. bis zum 15. Jahrhundert n. Chr. Praktisch zum Stillstand gekommen. Die arabische Renaissance usw. hat in der Zwischenzeit zwar wichtige Arbeit geleistet, aber in Bezug auf die physikalischen Wissenschaften waren das hauptsächlich Bestätigungen der Errungenschaften, die bereits zur Zeit des kyrenäischen Ammontempels und der Akademie von Athen im 4. Jahrhundert v. Chr. erreicht worden waren. Man darf diese Bestätigungen nicht abwerten, aber man darf diese relativen Verdienste auch nicht mit allgemeinen Fortschritten in der menschlichen Geistesgeschichte verwechseln.
Die Genialität der westlichen jüdisch-christlichen Zivilisation, veranschaulicht durch den Einfluß von Philo von Alexandria auf das Judentum und die Verteidigung des Werks der Apostel (gegen den byzantinischen Gnostizismus) durch den heiligen Augustinus, ist die wesentliche Kraft, ohne die die große Explosion des wissenschaftlichen Fortschritts insbesondere seit dem Werk des Nikolaus von Kues im 15. Jahrhundert nicht möglich gewesen wäre.
Dieser spezifische Genius der jüdisch-christlichen Kultur findet sich zum Teil im Gebot der Schöpfungsgeschichte an die Menschheit: „Seid fruchtbar und mehret euch, füllet die Erde und machet sie euch untertan.“ Dies ist ein Gebot, das Juden und Christen auffordert, sich dem technischen Fortschritt zu widmen. Die Möglichkeit eines nachhaltigen wissenschaftlich-technischen Fortschritts wurde bereits durch Platons Akademie in Athen – der von Solon in Athen – aufgezeigt, und zwar konzentriert in Platons Dialog Timaios, worin gezeigt wird, daß sich die Prinzipien der schöpferischen wissenschaftlichen Entdeckung mit einer bestimmten Art von Monotheismus, dem Monotheismus von Philo und den christlichen Aposteln, decken.
Bei Platon wird das Prinzip der Hypothese der höheren Hypothese als die Tätigkeit definiert, durch die die Menschheit die Übereinstimmung zwischen dem menschlichen Wissen und dem universellen Willen Gottes, dem Logos, der Konsubstantialität des Schöpfers und den gesetzmäßigen, universalen Prinzipien der effizienten Zusammensetzung des Universums vervollkommnen kann. Augustinus, der das Filioque-Prinzip der westlichen lateinischen Liturgie formulierte, definiert Christus als den vervollkommneten Zustand des sterblichen Seins, so daß der Wille des Schöpfers, des Logos, genauso von Christus wie vom Schöpfer ausgeht, und daß es aus diesem Grund die erste Pflicht der Menschheit ist, in der Nachfolge Christi zu leben.
Die Einbindung dieser jüdisch-christlichen Kultursicht in die republikanischen Strömungen der westlichen Zivilisation seit der Zeit des Augustinus verlieh der westeuropäischen Zivilisation ein überlegenes Potential, sich den wissenschaftlichen Fortschritt anzueignen, da diese kulturelle Anschauung die geeignete Beziehung des sterblichen Menschen zum Schöpfer definierte, um dem Weg der Hypothese der höheren Hypothese zu folgen. Nikolaus von Kues und andere während der Goldenen Renaissance entfalteten dieses Potential immer weiter, wodurch die potentielle genialische Kraft der westeuropäischen Zivilisation während der letzten 500 Jahre freigesetzt wurde.
Die erneute Bestätigung dieses Menschenbildes der Goldenen Renaissance im Gegensatz zu dem hedonistischen materialistischen Standpunkt hat die Neigungen des Individuums in eine für wissenschaftliche Arbeit äußerst fruchtbare Richtung gelenkt – weg von der Sterilität des Empirismus und Positivismus, hin zum Standpunkt von Cusa, da Vinci, Kepler, Leibniz, Gauß, Riemann und anderen.
In dieser Hinsicht ist das Haupthindernis für den wissenschaftlichen Fortschritt heute nicht der Mangel an formaler Bildung, sondern das Fehlen einer entsprechenden moralischen Erziehung, das Fehlen eines persönlichen Identitätsgefühls, das mit der Hypothese der höheren Hypothese und der damit verbundenen „Innenorientiertheit“ einhergeht.
Sich für den Kampf gegen die Krankheiten des Alterns als zentralem Anliegen einer neuen, planvolleren Erforschung der Lebensprozesse einzusetzen, bestätigt somit das moralische Menschenbild, das für eine erfolgreiche wissenschaftliche Untersuchung in dieser Richtung unerläßlich ist. Es besteht ein Zusammenhang zwischen der moralischen Wahl seiner Arbeit und der Qualität des erreichten Ergebnisses.
Deutsche Erstübersetzung Dr. Wolfgang Lillge
Physiknobelpreis für Forschung der Quantenverschränkung verliehen
Alain Aspect, John F. Clauser und Anton Zellinger haben für ihre Arbeiten zur Quantenverschränkung den Nobelpreis für Physik 2022 erhalten.

Als Quantenverschränkung bezeichnet man die Tatsache, daß zwei Teilchen von Natur aus so miteinander verbunden sein können, daß sie gemeinsame Eigenschaften haben. Wenn zum Beispiel zwei Antiteilchen aus einer Null-Spin-Bedingung erzeugt werden, haben die beiden neuen Teilchen entgegengesetzte Spins. Oder die beiden Gammateilchen, die bei der Materie-Antimaterie-Annihilation eines Elektrons und eines Positrons entstehen, haben eine ähnliche Polarisation.
Diese verschränkten Teilchen haben keine rein individuellen Eigenschaften mehr, sondern befinden sich in einem Zustand, der grundsätzlich nicht vom Kontext des verschränkten Systems als Ganzes zu trennen ist. Trotz großer räumlicher Trennung zwischen Teilen dieses Systems definiert eine Messung oder Interaktion mit den „Teilen“ augenblicklich das Potential für nachfolgende Messungen des gesamten Systems offenbar neu.
Die Zustände der verschränkten Teilchen sind nicht bekannt, bis sie gemessen werden. Sobald beispielsweise der Spin oder die Polarisation eines Teilchens gemessen wird, ist der Zustand des anderen sofort bekannt. Daraus ergeben sich zum Beispiel Anwendungen im Bereich der Quantensicherheit.
Es scheint auch zu implizieren, daß es so etwas wie lokalen Realismus nicht gibt. Die Beobachtung, mit der die gemessene Eigenschaft der Teilchen bestimmt wird, läßt sich mit einem Würfelwurf vergleichen, und der Moment der Messung bewirkt, daß eine Wahrscheinlichkeitsverteilung sofort einen einzigen Zustand annimmt.
Albert Einstein betrachtete die Fähigkeit, durch die Messung eines Teilchens den Zustand eines weit entfernten Teilchens beeinflussen zu können, als „spukhafte Fernwirkung“. Er fragte sich, ob durch den Beobachtungsprozeß nicht ein von Natur aus zufälliger Zustand in sich zusammenbricht, sondern ob es noch unbekannte verborgene Variablen gibt, die den Zustand der Teilchen genauer bestimmen.
Der irische Physiker John Bell, ein Anhänger Einsteins, entwickelte daraufhin ein mögliches experimentelles Konzept, mit dem sich feststellen ließ, ob eine Theorie der verborgenen Variablen – wie die von Bohm 1952 entwickelte – möglich war.
Die umfassenderen Ergebnisse, zu denen die drei Nobelpreisträger gelangten, zeigten, daß die von Bell entwickelten Ungleichungen verletzt werden und daß man nicht auf einen lokalen Realismus in der Quantentheorie hoffen könne.
Bereits Nikolaus von Kues hatte etwas zu dem Problem der Messung von Teilen eines Ganzen zu sagen. In seinem Dialog Der Laie über den Geist schrieb er folgendes:
Philosoph: Wenn die Größe das vollständige Sein von allem anderen unterscheidet, so weiß man also nur dann etwas, wenn man alles andere weiß.
Der Laie: Du hast recht. Man weiß keinen Teil, wenn man nicht das Ganze weiß. Das Ganze gibt das Maß für den Teil ab. Schnitze ich einen Löffel Teil für Teil aus dem Holz heraus, so gebe ich, den Teil gestaltend, auf das Ganze acht, damit ich einen wohlgefügten Löffel herausbekomme. Der ganze Löffel, den ich im Geist erfaßt habe, ist das Urbild, auf das ich hinblicke, während ich einen Teil gestalte. Einen vollkommenen Löffel kann ich nur dann zuwege bringen, wenn jeder Teil sein Verhältnis in Hinordnung auf das Ganze bewahrt. Ebenso muß jeder Teil mit dem anderen verglichen seine Vollständigkeit behalten. Darum wird es nötig sein, daß für das Wissen von einem einzelnen vorher das Wissen vom Ganzen und seinen Teilen vorhanden ist. Wenn man also Gott, der das Urbild des Alls ist, nicht kennt, kann man offenbar nichts vom All wissen und ebenso, wenn man das All nicht kennt, kann man nichts von seinen Teilen wissen. Jedwedem Wissen geht das Wissen von Gott und von allen Dingen voraus.

