Einleitung
Die vorliegende theoretische Untersuchung war anfangs motiviert durch das Finden und Entwickeln einer leicht verständlichen Lösung im Bereich vereinheitlichter Quanten- und Gravitationstheorien. Es werden modellbasierte Methoden verwendet, die sich auf die strukturellen Beschreibungen von Makro- und Mikroprozessen konzentrieren. Dabei wurden von uns einige grundlegende Hypothesen aufgestellt.
Einige dieser Hypothesen betreffen die Art und Weise der Verknüpfungen von atomaren Teilchen durch noch kleinere Elementareinheiten. Sie führte zu einem überraschenden Verständnis der inneren Struktur und Konstruktion von Quarks, Neutronen, Protonen und komplexeren Atomkernen. Von diesem Zeitpunkt an konzentrierte sich unsere Forschungsarbeit hauptsächlich auf die modellgestützte Interpretation subatomarer Prozesse.
Dieser Artikel ist die erste deutsche Veröffentlichung in gekürzter Fassung der englischen Online- und Print-Ausgabe vom Juli 2020 auf arXiv1 sowie vom August 2020 im Journal of Modern Physics, Vol. 11 No. 8.2 Die bisher erzielten und im Artikel vorgestellten Ergebnisse sind neu in der Physik. Sie bestehen aus einem generischen Beschreibungsmodell für die Struktur von Atomkernen – YY-Modell genannt. Dieses Modell enthält zwei wichtige strukturelle Raumbinder (Pairing Space Link, PSL, und Triple Space Link, TSL), die aus der Anfangsphase des kosmologischen Urknalls stammen. Sie halten atomare Teile zusammen und sind an vielen bekannten Kernfusions- und Kernspaltungsprozessen beteiligt. Modifikationen an einigen bekannten atomaren Prozessen, einschließlich der Elektron-Positron-Vernichtung (Annihilation), sind notwendig und werden beschrieben. Die Entstehungsprozesse des Elektrons und Positrons werden neu betrachtet. Eine Neuinterpretation der starken Kräfte aus dem Standardmodell ist möglich und wird gegeben. Basierend auf den strukturellen Zusammenhängen konnte ein tieferes Verständnis für die Materie-Umwandlungen (Transmutationen), für die frühen kosmologischen Prozesse und (möglicherweise auch) für die dunkle Materie erreicht worden.
Alle wichtigen Ergebnisse dieser Arbeit sind die logischen Schlußfolgerungen aus den verwendeten Hypothesen zu den zwei strukturellen Raumbindern. Sie müssen noch durch weitere theoretische und experimentelle Arbeiten untersucht und verifiziert werden. Das in diesem Artikel postulierte Y-Teilchen als Begleitprodukt der Elektron-Positron-Vernichtung wird für die zukünftigen Untersuchungen eine wichtige Rolle spielen.
Pairing Space Link (PSL) – Einfacher Raumbinder von Quarks
Ausgangspunkt ist die konventionelle Beschreibung der Elementarteilchen, Up-Quark und Down-Quark, unter Berücksichtigung ihrer wesentlichen Eigenschaften: Ein Up-Quark besitzt 2/3 positive elektrische Ladung, während ein Down-Quark 1/3 negative elektrische Ladung besitzt. Folglich werden zwei grundlegende Baueinheiten wie folgt ausgearbeitet:
- Die Einheit „Yin“ entspricht einem Drittel der negativen Ladung, symbolisiert durch „ – “;
- Die Einheit „Yang“ entspricht einem Drittel der positiven Ladung, symbolisiert durch „ + “.
Diese beiden Einheiten, deren physische Existenz vermutet wird, ziehen sich gegenseitig an, und sie halten sich auch voneinander fern, so daß ein stabiler Zustand entsteht, indem sie „gepaart“ werden und eine Raumverbindung bilden, den sogenannten „Pairing Space Link“ (PSL), wie in Abbildung 1 beschrieben.

Unter Verwendung von Yin, Yang und PSL werden die Quarks wie folgt beschrieben:
- Ein Down-Quark enthält und materialisiert eine Yin-Einheit
- Ein Up-Quark enthält und materialisiert zwei Yang-Einheiten und eine Raumverknüpfung
Die Gestalt der geometrischen Formen von Up-Quark und Down-Quark ergibt sich aus Abbildung 2.
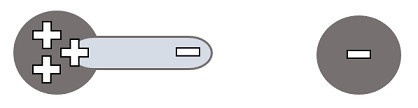
Der Unterschied des neuen Ansatzes zu dem Standardmodell der Physik besteht darin, daß das Yin-Yang-Pairing dem Up-Quark als Eigenschaft zur Raumbindung zugeordnet wird. Die elektrische Gesamtladung von einem Up-Quark sowie von einem Down-Quark bleiben im neuen Modell genauso wie im Standardmodell.
Neubetrachtung von Neutron und Proton
Nach dem Standardmodell besteht ein Neutron (elektrisch neutral) aus zwei Down-Quarks und einem Up-Quark. Hingegen besteht ein Proton (Wasserstoffkern 1H mit einer positiven Ladung) aus einem Down-Quark und zwei Up-Quarks. Die sogenannten Gluonen (wechselwirkende Teilchen) halten die Quarks zusammen, siehe Abbildung 3.
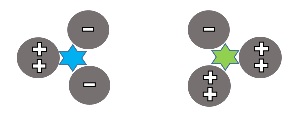
Durch Verwendung der Pairing Space Links gelangt das YY-Modell zur erweiterten Beschreibung von Neutron und Proton in Abbildung 4.

Die Nettosumme der positiven und negativen elektrischen Ladungen, jeweils für ein Proton und für ein Neutron, entsprechen der klassischen Beschreibung. Der einzige Unterschied besteht in den Pairing Space Links: sie halten den Kern zusammen – darin kann die Quantenchromodynamik des Standardmodells ihre Wurzeln finden.
Triple Space Link (TSL) – Komplexer Raumbinder von Quarks
Um komplexe Kerne zu modellieren, wurde ein weiteres Konstrukt, der „Triple Space Link“ (TSL), eingeführt. Er besteht aus drei PSLs, die sich auf ihren gemeinsamen Yang-Einheiten zusammenfinden. Ihr gemeinsamer Knoten entspricht einer positiven elektrischen Ladungseinheit („Dreifachladung“), siehe Abbildung 5 a.
In ähnlicher Weise können sich drei PSLs an ihren Yin-Einheiten zueinander binden, um eine negative elektrische Ladungseinheit zu bilden; siehe Abbildung 5 b.
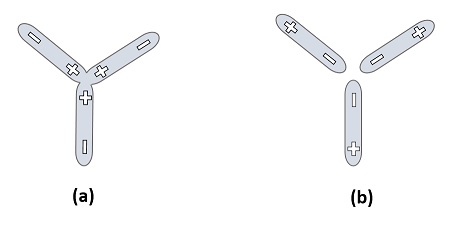
Es ist noch unklar, wie aus physikalischer Sicht drei Grundeinheiten eines gemeinsamen Zeichens in einem Knotenpunkt zum Aufladen verbunden werden. Darüber hinaus soll die dreifache Aufladung einen wesentlichen Unterschied zwischen den positiven und negativen Knoten in der Bindungsintensität ausmachen, wie in den Abbildungen 5 a und b dargestellt. Die Bindung am positiven Knoten ist stark, während die Bindung am negativen Knoten schwach ausgeprägt ist (dargestellt als Lücken) und während der Kerntransformationen immer wieder aufgelöst und mit Quarks verbunden wird. Diese Asymmetrie entspricht der Asymmetrie zwischen Down- und Up-Quarks, die sich auf die Ursprünge der Kosmologie zurückzuführen läßt.
Es gibt einige Regeln, die in den Kombinationen von Yin’s und Yang’s miteinander und mit den Quarks gelten, um ein konsistentes Atomkernmodell zu ergeben. Auf die Beschreibung dieser Regeln wird hier jedoch verzichtet.
Wir werden schnell feststellen, daß die Verwendung von PSLs und TSLs ein starkes Mittel ist, um die inneren Strukturen von Atomkernen auf konkrete Art und Weise zu beschreiben bzw. zu modellieren – dies geschieht um so filigraner, je komplexer die Atomkerne sind.
Wasserstoff-Atomkerne 2H und 3H, Neuinterpretation der Starken Kernkraft
Die Wasserstoff-Atomkerne 2H und 3H sind zwei Isotope des oben beschriebenen Wasserstoff-Kerns 1H: 2H (Deuterium) ist der Zusammenschluß eines Protons mit einem Neutron, während 3H (Tritium) aus einem Proton und zwei Neutronen zusammengeschlossen ist.
Zerlegt man ein Proton und ein Neutron in ihre Quarks und kombiniert sie durch Hinzufügen eines neuen TSL (Transmutation), so erhält man einen 2H-Atomkern, wie in Abbildung 6 dargestellt wird (Die Teile sind zur einfachen Identifizierung vor und nach der Transformation farblich gekennzeichnet).
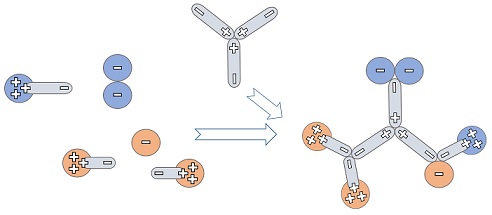
Des weiteren ist die Entstehung eines Tritiums (3H) aus einem Deuterium und einem weiteren Neutron unter Hinzunahme einer TSL in Abbildung 7 dargestellt.
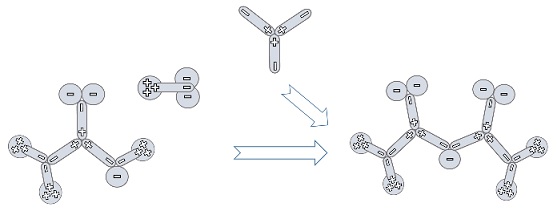
Die Beteiligung einer TSL am Prozeß der Neuzusammenstellung ist ein sehr wichtiger und neuer Aspekt im YY-Modell, mit mehr Details und mehr Kombinationsmöglichkeiten.
Die starken Kräfte des Standardmodells, die das Proton und das Neutron zusammenhalten, werden hier neu interpretiert: Die inneren negativen und positiven Dreifach-Ladungen der TSLs halten die umgebenden geladenen Up- und Down-Quarks zusammen – die Bindungskräfte selbst sind elektrostatische Kräfte. Die Quantenchromodynamik, die auf dynamischen Farbladungen von Quarks, Anti-Quarks und Gluonen sowie ihren Umwandlungen basiert, wird hier formal durch die Strukturen selbst neu interpretiert.
Zu beachten ist auch, daß hier die Zeichnung des atomaren Aggregats in einer zweidimensionalen Ebene erfolgt: Für eine realistische dreidimensionale Anordnung muß die elektrostatische Anziehung und Abstoßung der Up- und Down-Quarks um das gesamte Aggregat herum berücksichtigt werden. Im Fall von Abbildungen 6 und 7 müssen die doppelten Down-Quarks oben (oder/und die doppelten Up-Quarks links) senkrecht zur Ebene angeordnet sein, um elektrostatische Kräfte zu kompensieren.
Helium-Kern 4He
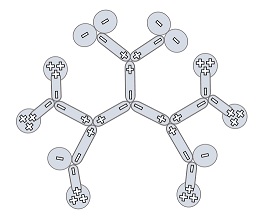
An dieser Stelle wird der Helium-Atomkern 4He im YY-Modell wiedergegeben, der aus zwei Protonen und zwei Neutronen aufgebaut ist (Abbildung 8). Auf dieses Modell wird in den Abschnitten über die Kernfusion noch zurückgegriffen.
Entstehung von Elektron und Positron
Kernfusionen können besser verstanden werden, wenn die Prozesse der Entstehung von Elektron und Positron sowie der Vernichtung der beiden beim Zusammentreffen (Annihilation) durch das YY-Modell präziser beschrieben werden.
Um ein Elektron zu erzeugen, berücksichtigt das YY-Modell formal die Wechselwirkung eines Neutrons mit einem TSL. Man erhält als Ergebnis ein Proton und drei „befreite“ Down-Quarks, die sich zu einem negativ geladenen Teilchen als Elektron zusammenschließen und dabei ein Antineutrino freisetzen, wie in Abbildung 9 dargestellt.
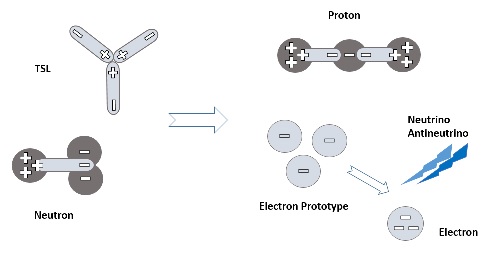
Das Standardmodell beschreibt diesen Prozeß als Beta-Zerfall (n → p+ + e– + –νe), während das YY-Modell dafür eine modifizierte Beschreibung liefert (n + TSL → p+ + e– + –νe). Der Hauptunterschied zwischen dem YY-Modell und den bekannten Prozessen im Standardmodell liegt in der Beteiligung eines TSL.
Die Entstehung eines Positrons wird durch den „umgekehrten Beta-Zerfall“ interpretiert (–νe + p → e– + n), wie in Abbildung 10 dargestellt. Dabei wandelt sich ein Proton durch Einwirkung eines Antineutrinos zu einem Neutron um und setzt ein Positron frei.
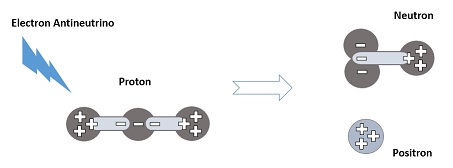
Aus der Perspektive des YY-Modells kann das Elektron aus drei tiefgebundenen Yin‘s eine kleinere Dimensionseinheit haben, als es unsere derzeitige physikalische Detektionsfähigkeit ermöglicht. Es gilt auch im YY-Modell, daß das Elektron ein „nicht teilbares Teilchen“ ist, und daß es beim Zusammentreffen mit einem Positron zur Vernichtung mit begleitender Gamma-Strahlung kommt. Es gibt jedoch einen wichtigen Unterschied: Im YY-Modell erzeugt diese Kollision einen wieder zusammengesetzten Dreifach-Raumbinder TSL (siehe nächster Abschnitt), der dem Raum „zurückgegeben“ wird und zu einer „Abfall“-Materie wird.
Elektron-Positron-Vernichtung im YY-Modell, Ergebnis TSL und Y-Teilchen
Das YY-Modell konserviert die an allen Transformationsprozessen beteiligten Yin‘s und Yang‘s. Die im Standardmodell beschriebene Elektron-Positron-Annihilation (e+ + e–→ 2 ɣ) wird im YY-Modell durch die Erzeugung eines TSL erweitert (e+ + e–→ 2 ɣ + TSL), die dieser Konservierung gehorcht, siehe Abbildung 11.
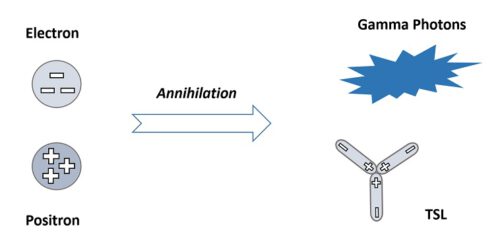
Das TSL ist eine Vorhersage des YY-Modells („Y-Teilchen“). Man kann es sich als Asche vorstellen, nachdem das Holz ausgebrannt ist. Jedes TSL hat eine Masse – definiert als eine „TSL-Masseneinheit“, die viel kleiner als die Masse von Elektron und Positron sein muß, aber dennoch nicht vernachlässigbar ist. Es könnte möglich sein, sie indirekt zu bestimmen, indem man eine genauere Energie-Masse-Balance zwischen den Vorhersagen und Beobachtungen verwendet, um auch den absoluten Wert der TSL-Masseneinheit abzuschätzen bzw. zu bestimmen.
Tatsächlich ist die Elektron-Positron-Annihilation Teil des Energie-Materie-Lebenszyklus, und die TSLs kehren zu der ursprünglichen Form der Materie zurück, die zu Beginn der kosmologischen Evolution als allererste entstanden ist. Darüber hinaus bildet die TSL-Bildung die Grundlage für die Antimaterie-Systematik des YY-Modells.
Stellarer Kernfusionsprozeß
Das Verständnis für atomare Fusionsprozesse verbessert sich durch das YY-Modell deutlich, nachdem wir jetzt die atomaren Bindungen in den TSLs identifiziert haben und die einzelnen Prozesse verschiedener Fusionen intuitiv und graphisch beschreiben können.
Im folgenden werden die drei wichtigsten stellaren Fusionsprozesse in Bezug auf das YY-Modell zusammengefaßt, ohne auf die Details einzugehen. Sie charakterisieren die Entstehung eines sonnenähnlichen Sternes aus den nach dem Urknall entstandenen Wasserstoffatomen, die sich im Raum durch die Gravitationswirkungen zusammenschließen.
Kernfusion zu Deuterium 2H
Im Anfangsstadium der stellaren Kernfusion wird ein Wasserstoff-Isotop 2H durch Verschmelzung zweier Protonen 1H erzeugt. Betrachtet man diesen Prozeß zusammen mit den zugehörigen Elektronen, dann sind rechnerisch immer zwei Wasserstoffatome notwendig. Unter hohem energetischen Druck wandelt sich ein Proton in ein Neutron und ein Positron. Dieses wird zusammen mit einem der zwei Elektronen vernichtet und dabei Gamma-Strahlung und ein TSL freisetzt. Der freigesetzte TSL bindet dann das andere Proton und ein durch das erste Proton umgewandeltes Neutron zu einem 2H-Kern zusammen (2 1H + 2 e– , ionisiert u. energetisiert → 2 ɣ + 2H + e–).
Kernfusion zum Heliumisotop 3He
Auf der nächsten Stufe der stellaren Kernfusion wird ein Heliumisotop 3He erzeugt, indem ein Proton 1H und ein Wasserstoff-Isotop 2H miteinander verschmelzen. Nach dem YY-Modell ist ein neuer TSL erforderlich, der durch die Annihilation eines Elektrons und eines entstandenen Positrons zusammen mit der Gamma-Strahlung freigesetzt wird (1H + 2H + 2 e– , ionisiert u. energetisiert → 2 ɣ + 3He + e–).
Kernfusion zu Helium 4He
In einer weiteren Stufe der stellaren Kernfusion werden ein stabiles Helium 4He und zwei Protonen 1H durch Verschmelzung zweier Heliumisotope 3He erzeugt (3He + 3He → 4He + 2 p + 12,9 MeV). Interessanterweise wird in dieser Fusionsstufe kein TSL verbraucht. Im Gegenteil wird ein TSL freigesetzt, der in den beiden frühen Fusionsstufen für 2H und 3He wiederverwendet werden kann. Mit anderen Worten, die Gamma-Strahlung wird eher in den ersten beiden Fusionsstufen erzeugt.
Die TSL-Entstehung und seine Beteiligung an den Kernfusionsprozessen ist im Vergleich zum Standardmodell neu und von großer Bedeutung. Der TSL ist nicht leicht nachweisbar und daher bisher außerhalb des Fokus unserer Experimentalphysik. Es handelt sich um einen stabilen Zustand der Materie.
Kernspaltung und Freisetzung von TSLs
Ein wesentlicher Vorgang im Zusammenhang mit einem Kernspaltungsprozeß findet an der Spaltungsstelle statt. Am Beispiel der Kernspaltung von Uran-Atomen
n + 235U → 139Ba + 95Kr + 2 n + 200 MeV
wird dargestellt, welche Produkte sich aus der Spaltung ergeben. Das YY-Modell beschreibt diese Trennungsstelle mit einer möglichen Strukturkonfiguration vor und nach der Trennung in Abbildung 12. Farbige Teile helfen, sie in der Struktur des großen Kernstücks vor und der kleinen Kernstücke nach der Spaltung zu identifizieren.
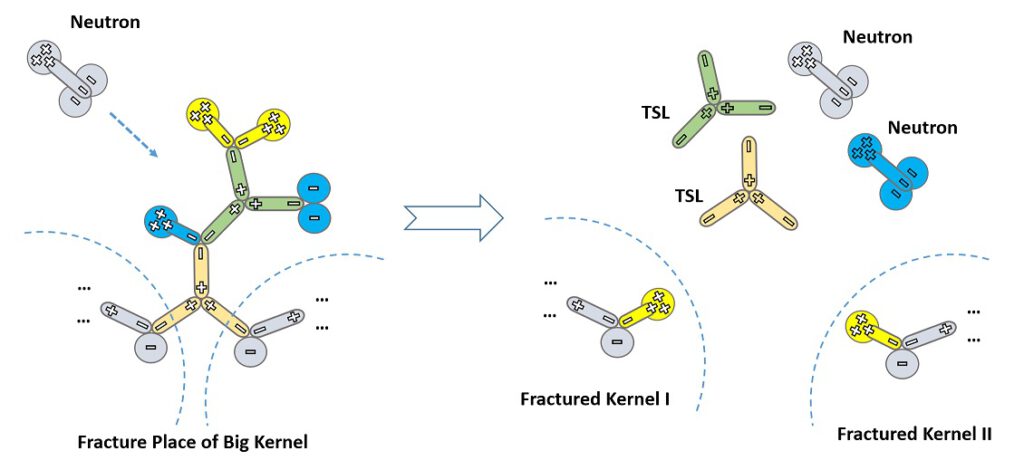
Es bleiben nicht nur Up- und Down-Quarks erhalten, sondern auch die elektrischen Ladungen vor und nach der Trennung. Außerdem werden zwei bestehende TSLs freigesetzt.
Kalte Fusion
Das YY-Modell liefert zusätzliche Argumente, die helfen können, zu verstehen, ob und wie die sogenannte Kalte Fusion funktioniert.
Eine Kernreaktion ohne Verbrauch von TSL kann als „kalt“ betrachtet werden, da keine Elektron-Positron-Vernichtung stattfindet und daher keine Gammastrahlung erzeugt wird. Transformationsprozesse, die sogar TSLs freisetzen (wie es beim Helium-Verschmelzen oder beim Uran-Spalten der Fall ist), liefern diese für parallel ablaufende Fusionen, die TSLs zum Binden verbrauchen (konsumieren). Stellare Fusionsprozesse, die TSLs zur Bindung benötigen, wie bereits für die Bildung von 2H und 3He beschrieben, können für sich selbst die TSLs in Begleitung für die Gamma-Strahlungen „produzieren“.
Es ist möglich, daß andere große Atomkerne (nicht unbedingt Uran) bei der Spaltung ebenso TSLs freisetzen, so daß diese TSLs durch parallel ablaufende Fusionen ohne oder mit wenig Gamma-Strahlung verbraucht werden können.
Die folgende Abbildung 13 ist die YY-Modellbeschreibung für den bekannten Kernfusionsprozeß zu Helium 4He aus Deuterium und Tritium: 2H + 3H → 4He + 3,5 MeV + (n + 14,1 MeV)
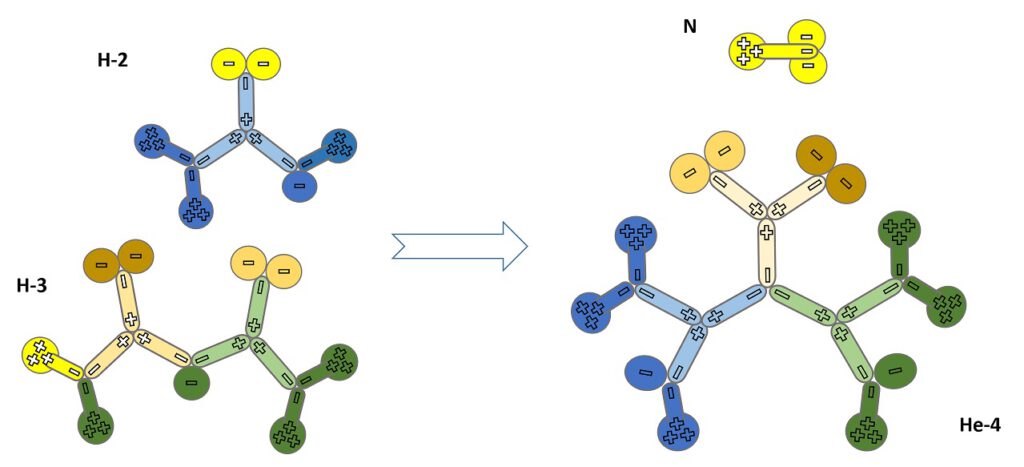
An diesem Prozeß ist kein TSL beteiligt, weder verbraucht noch freigesetzt. Gamma-Strahlung tritt nicht auf. Daher ist die Wasserstofffusion von 2H und 3H zu Helium 4He ein guter technischer Kandidat für die kalte Kernfusion, die für Anwendungen zur Energiegewinnung interessant ist.
Schlußfolgerung und Ausblick
Das YY-Modell eröffnet ein breites Spektrum für die theoretische und experimentelle Forschung in der Atomphysik und Molekularchemie. Auf der Grundlage der detaillierten Konstruktionsstruktur des Atomkerns und seiner Varianten sollen elektrostatische und Quantenfeldberechnungen filigranere Ergebnisse liefern können, als dies derzeit möglich ist. Zum Beispiel: Wie wird die dreidimensionale Struktur eines schweren Atomkerns durch elektrostatische Wechselwirkungen von Quarks in einigen Teilen zusammengezogen und in anderen Teilen gedehnt oder gefaltet.
Bislang sind die maßgeblichen Kräfte für den PSL und TSL noch Hypothesen. Ein möglicher Weg, ihnen eine Grundlage zu geben, besteht darin, sie mit der Quantenchromodynamik-Interpretation zu kombinieren. Alternativ können ähnliche Methoden aus der Quantenchromodynamik verwendet werden, um die notwendigen Wechselwirkungen im YY-Modell zu klären. Die Idee, daß die Teilchenwechselwirkungen auf den zyklischen Gruppen Z2 (Ladungen, materialisiert durch die PSLs) und Z3 (Farben, materialisiert durch die TSLs) basieren, kann für zukünftige Analysen aus diesem Modell abgeleitet werden.
Die Verteilung von Elektronenwolken in Orbitalen um den Atomkern wird ebenfalls von Bedeutung sein. Ein detaillierteres Atommodell wird weitere Details der Orbitale sowie bisher verborgene Strukturen auf molekularer Ebene zu Tage fördern. Ein Isotop eines Atoms kann im YY-Modell verschiedene Kernstrukturkonfigurationen haben. Die Suche nach Unterschieden in den physikalischen und chemischen Eigenschaften kann interessante Aspekte aufdecken und zur Erforschung radioaktiver Zerfallsprozesse beitragen. Die mögliche Beziehung des YY-Modells zum bestehenden Preon-Modell ist eine offene Frage. Im Preon-Modell wird die Komposition als Substruktur über das Standardmodell hinaus vorgeschlagen.
Fußnote(n)
