1. Einleitung
In den letzten 150 Jahren stieg die globale Mitteltemperatur nach Angaben des Hadley Centers um ungefähr 1,3 °C (s. Abbildung 1.0). Dabei werden bei der Darstellung der zeitlichen Änderung der globalen Mitteltemperatur aus Genauigkeitsgründen nur die Abweichungen angegeben. Die Festlegung auf Absolutwerte wird vermieden, da die Zahl, Qualität und Lage der Meßstellen keine genauere Ermittlung erlauben. Trotzdem hat die NOAA die mittlere globale Durchschnittstemperatur im Referenzzeitraum 1951–1980 mit einer Genauigkeit von ± 0,5 °C zu 14 °C entsprechend 287 K, angegeben. Damit liegt die heutige mittlere globale Temperatur bei 288 K.
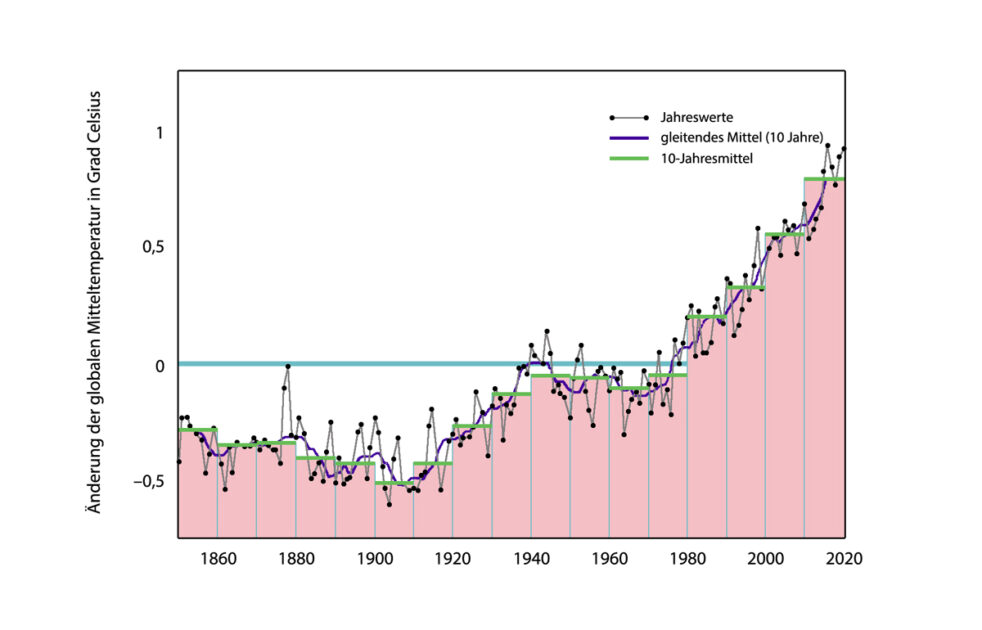
Parallel zur globalen Mitteltemperatur stieg die Kohlendioxidkonzentration von 310 ppm im Jahr 1955 auf 415 ppm im Jahr 2020 (s. Abbildung 1.1). Es liegt nahe, den Temperaturanstieg mit dem Anstieg der Kohlendioxidkonzentration in der Atmosphäre zu korrelieren. Für diese Korrelation bestehen zwei Möglichkeiten der Interpretation von Ursache und Wirkung:
- Der Anstieg der Kohlendioxidkonzentration in der Atmosphäre ist die Ursache für die Temperaturerhöhung, oder:
- Eine durch andere Einflußgrößen verursachte Temperaturerhöhung hat den Anstieg der Kohlendioxidkonzentration in der Atmosphäre zur Folge. Dieser ist dann nur eine Reaktion und als Regelgröße für Maßnahmen zur Einflußnahme auf das Klima völlig ungeeignet.
Während die erste mögliche Interpretation in den letzten Jahren zunehmend Eingang in die Politik gefunden hat und riesige finanzielle und forschungsbezogene Anstrengungen zur Verhinderung einer angeblichen Klimakatastrophe zur Folge hatte, blieb die zweite Möglichkeit der Interpretation bisher weitgehend unberücksichtigt.
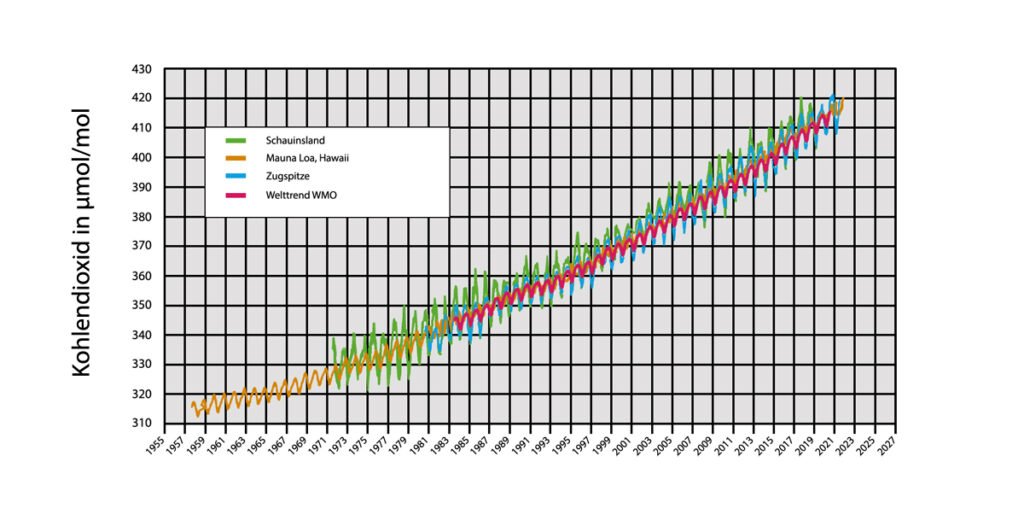
Trotz aller Aufwendungen und trotz eines unfreiwilligen, beispiellosen Modellversuchs zur Reduktion der durch menschliche Aktivitäten erzeugten Menge an Kohlendioxid während der weltweiten „Lockdown“-Phasen im Rahmen der Corona-Infektionswellen stieg und steigt der Kohlendioxidgehalt der Atmosphäre unbeirrt weiter, wie Abbildung 1.1 zeigt.
Zweifel an der Annahme, daß eine steigende Kohlendioxidkonzentration in der Atmosphäre die Ursache für die steigende globale Temperatur ist, sind angezeigt. Die oben erwähnte Alternative einer Erhöhung der Kohlendioxidkonzentration der Atmosphäre als Folge der Erderwärmung erscheint wahrscheinlicher. Damit rückt eine gestiegene Energieaufnahme des Systems Erde als Erklärung für die Erderwärmung in den Vordergrund.
Abgesehen von einer geringen durch radioaktive und chemische Prozesse im Erdinneren erzeugten Menge bezieht die Erde ihre Energie von der Sonne. Diese liefert jährlich mit geringen Schwankungen eine vorwiegend im kurzwelligen Bereich erfolgte mittlere Strahlungsleistung von 1365 Watt/m2 (Solarkonstante) auf eine der Sonne zugewandten, auf eine Kreisscheibe projizierten Erdoberfläche.
Die Erklärung klimatischer Änderungen im System Erde (Atmosphäre und Erdoberfläche) erfolgte bisher überwiegend über die Bilanz von Einstrahlung der Sonne und Abstrahlung der Erde. Dabei wird davon ausgegangen, daß ein Betrag von ungefähr 30 Prozent der auftreffenden Strahlungsleistung der Sonne ohne klimatische Wirkung reflektiert wird. Bei dieser Reflexion beträgt die Reduktion der Einstrahlung der Sonne ungefähr 409 Watt/m2. Dieser, als Albedo bekannte Betrag, wird bei Betrachtungen von Klimaveränderungen allgemein als zeitlich konstant angenommen, was bei veränderten Verhältnissen in der Atmosphäre und am Erdboden nicht korrekt ist. Allein zwischen 1998 und 2017 sank der Wert für die Albedo um 0,5 Watt/m2, wie P. R. Goode et al. über Messungen des Erdscheins festgestellt haben.1
Ausgehend von dieser fraglichen Annahme bleiben für das System Erde ungefähr 960 Watt/m2, die auf eine viermal so große Fläche der Erdkugel verteilt werden, da die Kugel eine um den Faktor 4 größere Fläche als der Kreis mit dem gleichen Radius hat. Damit ergibt sich ein Wert von ungefähr 240 Watt/m2 für die Einstrahlung, verteilt auf die Fläche der Erdkugel.
Stabile Verhältnisse im System Sonne/Erde werden nur erreicht, wenn die Einstrahlung der Sonne der Abstrahlung der Erde entspricht. Die Stefan-Boltzmann-Gleichung ergibt für die Strahlungsleistung von 240 Watt/m2 eine Temperatur des Strahlers von ungefähr 255 K an, die um ungefähr 33 K unter der über das Jahr gemittelten Temperatur der Erdoberfläche von 288 Kelvin, entsprechend 15 °C, liegt.
Zur Erklärung dieser Diskrepanz wird mit der Gegenstrahlung durch sogenannte „Treibhausgase“ in der Atmosphäre argumentiert, zu denen Kohlendioxid gehört, das als maßgeblicher Treiber angesehen wird. Diese Gegenstrahlung soll dann eine ausgeglichene Strahlungsbilanz auf der Erdoberfläche bewirken.
Dazu erklärte die Deutsche Physikalische Gesellschaft gemeinsam mit der Deutschen Meteorologischen Gesellschaft 1987 in einem Aufruf:
„Der Gehalt an Kohlendioxid und Wasserdampf hat eine entscheidende Rückwirkung auf das Klima: Ohne diese Gase würde aufgrund der Strahlungsbilanz zwischen Einstrahlung von der Sonne und Abstrahlung von der Erde die mittlere Temperatur auf der Erde etwa –18 °C betragen. Diese Gase absorbieren einen Teil der von der Erdoberfläche abgestrahlten Wärme und strahlen diese wieder teilweise zurück – Treibhauseffekt –, so daß die mittlere Temperatur gegenwärtig +15 °C beträgt.“
Hier wird die Temperaturdifferenz allein mit Strahlungs- und Absorptionsvorgängen erklärt, ohne zu berücksichtigen, daß in der Atmosphäre nicht nur die Strahlungsbilanz entscheidend für die Gleichgewichtstemperatur ist. Die Summe aus thermischer Energie, Gravitationsenergie (potentieller Energie) und Strahlungsenergie ist eine Erhaltungsgröße im System Erdoberfläche und Atmosphäre!
Als Folge dieser Betrachtungsweise rückt die Energieaufnahme des Systems Erde in den Vordergrund. Ändert sich die jährliche effektive solare Einstrahlung, der wirksame Energieeintrag, so ändern sich die klimatischen Verhältnisse auf der Erde so lange, bis sie einen neuen Gleichgewichtszustand erreicht haben.
2. Die Erde und ihre Atmosphäre
Die Erde ist der einzige Planet im Sonnensystem, an dessen Oberfläche Wasser in flüssiger Form bestehen kann und der ausreichend Masse hat, eine Atmosphäre festzuhalten, die auch thermodynamischen Gesetzen folgt und in der sich Wolken aus Wasserdampf bzw. Eiskristallen bilden können.
Vom Weltall betrachtet ist die Erde ständig zu ungefähr 2/3 von Wolken umhüllt.
2.1. Die Erdoberfläche
Ungefähr 365 der 511 Millionen km2 der Erdoberfläche sind von Ozeanen bedeckt. Der Rest sind Landmassen. Aktuell sind von der restlichen Fläche (ungefähr 146 Millionen km2) ungefähr 104 Millionen km2 bewohnbares Land, 15 Millionen km2 sind von Eis bedeckt, 27 Millionen km2 bestehen aus Sand und Salzwüsten, Hochgebirge, Stränden und Dünen. Das bewohnbare Land wird zu 50 Prozent, also ungefähr 51 Millionen km2, landwirtschaftlich genutzt, 39 Millionen km2 sind Wälder, 12 Millionen km2 von Sträuchern und Büschen bewachsen, 1,5 Millionen km2 werden für menschliche Ansiedlungen genutzt, und weitere 1,5 Millionen km2 bedecken Süßwasser-Flüsse und -Seen. 40 Millionen km2 des landwirtschaftlich genutzten Landes sind Wiesen, der Rest von 11 Millionen km2 dient dem Getreideanbau.2
Zählt man alle Tropenwälder zusammen, also die tropischen Regen- und Trockenwälder und die laubabwerfenden Monsunwälder, summiert sich der Tropenwald auf ungefähr 17,7 Millionen km2. Allein ungefähr 10 Millionen km2 bedeckt heute der tropische Regenwald.3
Abbildung 2.1 zeigt die Nutzungsänderung der Landfläche der Erde von 1750 und 1990 nach Ramakutty und Foley 1999.4
Vor Beginn der Industrialisierung, die für die Jahre nach 1750 angenommen wird, schätzt man das landwirtschaftlich genutzte oder beweidete Land auf ungefähr 9 Millionen km2 der Erde. Der globale Waldbestand wird für das Jahr 1750 zu 52 Millionen km2, die Wüsten-, Salzflächen, Strände und Hochgebirge können als gleichbleibend bei 27 Millionen km2 angenommen werden, so daß von ungefähr 42 Millionen Quadratkilometern Steppen- und Strauchland ausgegangen werden kann. Auch die Eisflächen werden gleichbleibend auf ungefähr 15 Millionen km2 geschätzt.
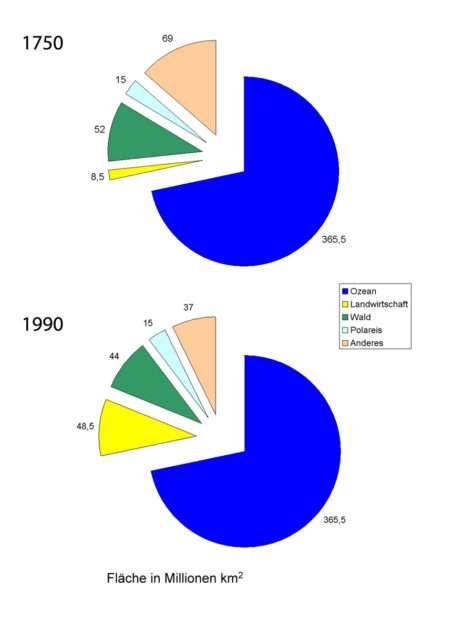
Bis 1990 dehnte sich die Fläche des Acker- und Weidelandes auf 48,5 Millionen km2 aus. Die Ausdehnung erfolgte überwiegend zu Lasten des Steppen- und Strauchlandes sowie des tropischen Regenwaldes. Der Waldbestand ging um ungefähr 8 Millionen auf 44 Millionen km2 zurück. Heute wird der Waldbestand mit ungefähr 40 Millionen km2 angegeben. Von 1990 bis 2021 ist eine Fläche von ungefähr 2 Millionen km2 Tropenwald gerodet worden, ungefähr 50 Prozent der Abnahme des weltweiten Waldbestandes.
Land- und Wasserflächen sind auf der Erdkugel ungleichmäßig verteilt. Die Fläche der Nordhalbkugel setzt sich aus 39 Prozent Landfläche und 61 Prozent Wasserfläche, die der Südhalbkugel aus 19 Prozent Landfläche und 81 Prozent Wasserfläche zusammen. Auch die Besiedelung der Erde mit ihren zivilisatorischen Veränderungen der Erdoberfläche ist zwischen Nordhalbkugel und Südhalbkugel sehr unterschiedlich. Auf der Nordhalbkugel leben ungefähr 90 Prozent der Erdbevölkerung von derzeit etwa 8 Milliarden Menschen.
Durch Besiedelung und der damit verbundenen Versiegelung der Erdoberfläche (worunter man die luft- und wassserdichte Abdeckung des Bodens versteht) kommt eine zusätzliche Veränderung der Erdoberfläche hauptsächlich in der Nordhalbkugel hinzu. Die Versiegelung der Erdoberfläche hat heute weltweit bereits eine Fläche von ungefähr 250 Millionen Hektar oder 2,5 Millionen km2 erreicht. Bis zum Jahr 2050 wird auf Grund des Bevölkerungswachstums mit einer Steigerung auf 4,2 Millionen km2 gerechnet.5
Die aktuellen 2,5 Millionen km2 versiegelte Fläche setzt sich u. a. aus ungefähr 1 Millionen km2 Straßen und Wegen, ungefähr 1 Millionen km2 Dachflächen und befestigten Außenflächen sowie Industrieanlagen zusammen.
Diese Zahlen zeigen, daß sich die Oberflächenbeschaffenheit der Erde seit 1750 deutlich verändert hat, besonders in der jüngsten Vergangenheit.
Wälder und Ackerflächen sowie versiegelte Flächen haben ein unterschiedliches Reflexionsvermögen für die Sonneneinstrahlung. Versiegelte Flächen sind zusätzlich vom natürlichen Wasserkreislauf (Verdunstung) ausgeschlossen.
2.2. Die Erdatmospäre
Die Erdatmosphäre besteht aus einem kompressiblen Gas, der Luft, welches sich im wesentlichen aus 78 Prozent Stickstoff, 21 Prozent Sauerstoff, 0,9 Prozent Argon und ungefähr 0,04 Prozent Kohlendioxid und Wasser in molekularer oder kondensierter Form zusammensetzt. Die Dichte ρ0 der Luft hat an der Erdoberfläche einen Wert von 1,29 g/m3 und erzeugt mit ihrer über die Erde verteilten Masse von 5,14 · 1018 kg einen Druck P0 von 1013 hPa (1 hPa = 100 Pa; 1 Pa = 1 kg/m · sec2) auf die Erdoberfläche. Zunehmende Höhe H, führt zu einer exponentiellen Abnahme des Luftdrucks, entsprechend der barometrischen Höhenformel:
PH = P0 · e–P0 · g · H/P0 [2.2]
Mit den angeführten Werten für die Dichte der Luft und den Druck, beides auf Meereshöhe gemessen, und g = 9,81 m/sec2 der Erdbeschleunigung ergibt sich für den Druckabfall auf die Hälfte des Ausgangswertes die Halbwertshöhe HM = 5550 m.
Damit liegen 50 Prozent der Luftmasse der Atmosphäre zwischen dem Meeresspiegel und der Höhe HM. HM kann auch als Höhenlage einer auf eine Ebene geschrumpften Masse der Atmosphäre interpretiert werden.
An der Troposphärengrenze, die im Mittel bei einer Höhe von 11.000 m liegt, ist der Luftdruck bereits auf ungefähr 25 Prozent des Ursprungswertes abgefallen.
Die barometrische Höhenformel beschreibt das Verhalten eines Gases unter dem Einfluß der Erdanziehung, wenn die Temperatur als konstant angenommen wird.
Die Temperatur in der Troposphäre verändert sich jedoch mit wachsender Entfernung von der Erdoberfläche. Sie fällt von einer über das Jahr gemittelten Temperatur von ungefähr 288 K, entsprechend 15 °C auf ungefähr 220 K, entsprechend –53 °C am Beginn der Tropopause, die an der Troposphärengrenze beginnt. Danach bleibt die Temperatur in der Tropopause über mehrere Kilometer Höhenanstieg weitgehend konstant.
2.2.1. Thermodynamik der Erdatmosphäre
Aus dem ersten Hauptsatz der Thermodynamik lässt sich die adiabatische Druck- und Temperaturabhängigkeit eines Gases ableiten.6
T0/TT = (P0/PT) 1 – 1/κ [2.2.1]
Dabei stellt κ den Adiabatenexponenten κ = cp/cV dar, dem Quotienten aus der spezifischen Wärme des Gases bei konstantem Druck cp und konstantem Volumen cV.
Bei adiabatischen Prozessen ist die Summe aus thermischer und potentieller Energie eine Erhaltungsgröße und führt mit Hilfe der barometrischen Höhenformel zu der Gleichung
T0/TT= e P0 · g · HT (κ – 1)(P0 · κ) [2.2.2]
Verschoben in die Höhenlage einer auf eine Ebene geschrumpften Masse der Atmosphäre läßt sich diese Gleichung in der Form schreiben:
TH = TM · e P0 · g · (HM– H)(κ – 1)(P0· κ) [2.2.3]
Dabei ist TM die Temperatur der auf eine Ebene geschrumpften Masse der Atmosphäre.
Mit dem Adiabatenexponenten κ = 1,4 wird ein ideales Gas (wie trockene Luft) beschrieben. Bei feuchter Luft kommt es beim Aufsteigen und Abkühlen zur Kondensation. Durch die freiwerdende Kondensationswärme wird der Exponent niedriger. Das Verhalten der Atmosphäre wird am besten durch einen Adiabatenexponenten von 1,23 angenähert.
Für die Halbwertshöhe des Luftdrucks HM = 5550 m, ergibt sich aus Gleichung 2.2 mit den im vorhergehenden Kapitel genannten Werten für die Dichte der Luft (ρ0 = 1,29 kg/m3), dem Luftdruck auf Meereshöhe (ρ0 = 1013 hPa) sowie der Erdbeschleunigung (g = 9,81 m/sec2) für T0/TM = 1,14. Wird für T0 = 288 K eingesetzt, die mittlere Temperatur der Erdoberfläche, so ergibt sich eine Temperatur von TM = 252,6 K für die Luftschicht in der Höhe HM = 5550 m. In der auf eine Ebene geschrumpften Masse der Atmosphäre herrscht damit eine Temperatur von ungefähr 253 K.
Ein Gedankenexperiment verdeutlicht diesen Prozeß:
Bei einer Erdkugel, deren Atmosphäre durch andere als die Gravitationskräfte festgehalten wird, hat die Luftschicht eine von der Höhe unabhängige Dichte. Sie ist überall gleich und soll überall die gleiche Temperatur von TM = 253 K, die Temperatur der Halbwertshöhe HM haben.
Wird die Gravitation „dazu geschaltet“, so erfolgt durch die Schwerkraft eine Dichte- und Druckzunahme in Richtung Erdmittelpunkt und eine Dichte- und Druckabnahme in Richtung der oberen Grenze der Atmosphäre.
Dieser Vorgang entspricht einer adiabatischen Expansion nach oben und einer adiabatischen Kompression nach unten. Es kommt in Richtung der Erdoberfläche zur Erwärmung von 253 K auf 288 K und in entgegengesetzter Richtung zur Abkühlung von 253 K auf 222 K bei einer Höhe von 11.100 m.
Durch die adiabatische Kompression unter dem Einfluss der Schwerkraft erhöht sich die Temperatur der Luft an der Erdoberfläche von 253 K auf 288 K. Die Temperatur an der Troposphärengrenze reduziert sich auf 222 K.
Es ist also keine Gegenstrahlung erforderlich, um die Temperaturdifferenz zwischen der Strahlungsgleichgewichtstemperatur und gemessenen gemittelten Temperatur der Erdoberfläche zu erklären.
3. Die Sonne
Abgesehen von einer geringen, durch radioaktive und chemische Prozesse im Erdinneren erzeugten Menge, bezieht die Erde ihre Energie von der Sonne.
Mit großer Näherung folgt die Strahlungsleistung der Sonne dem Planckschen Strahlungsgesetz.
R(λ,T) = (2 π c2 h)/λ5 · 1/(eh c/λ k T – 1) [3.1]
R(λ,T) beschreibt die spektrale Strahlungsleistung in (Watt/m2 · µm). Dabei ist h das Plancksche Wirkungsquantum (h = 6,62606896 · 10–34 J · sec), c die Lichtgeschwindigkeit im Vakuum (c = 2,9979246 · 108 m/sec), k die Boltzmann-Konstante (k = 1,3806504 · 10–23 J/K) und λ die Wellenlänge der Strahlung, angegeben in Mikrometer (µm). T ist die Temperatur des Strahlers in K (d. h. °K, wobei 0 °C = 273 K).
Die Integration der spektralen Strahlungsdichte über alle Wellenlängen der ausgesandten Strahlung liefert die Strahlungsflußdichte und das Gesetz von Stefan und Boltzmann:
S(T) = σ · T4 [3.2]
Die Strahlungsflußdichte S(T) steigt mit der vierten Potenz der Temperatur eines Strahlers. σ ist die Stefan-Boltzmann-Konstante:
σ = (2 π5 k4)/(15 h3 c2) = 5,670 · 10–8 W/(m2 · K4) [3.3]
Mit T = 5778 K, der Oberflächentemperatur der Sonne, ergibt sich daraus die Strahlungsflußdichte der Sonne an der Sonnenoberfläche zu 63.000 kW/m2.
Die Strahlungsflußdichte verringert sich quadratisch mit der Entfernung von der Quelle. Damit ergibt sich mit dem Wert für den Radius der Sonne (6,95 · 105 km) und der Entfernung der Erde von der Sonne (gemittelt 1,496 · 108 km) die Strahlungsflußdichte am Ort der Erde im Weltall, die Solarkonstante, zu:
SE = (RS/RE S)2 · PS = 1365 W/m2 [3.4]
Abbildung 3.0 zeigt die Wellenlängenabhängigkeit der spektralen Strahlungsdichte für die auf eine Kreisscheibe projizierte Erde. Im ultravioletten Bereich der Sonnenstrahlung (0,1–0,4 µm) beträgt die Strahlungsflußdichte ungefähr 108 Watt/m2, bei der die UVA-Strahlung (0,3–0,4 µm) mit 84 Watt/m2 überwiegt. Im Bereich des sichtbaren Lichtes (0,4–0,76 µm) erreichen ungefähr 610 Watt/m2 den oberen Rand der Erdatmosphäre, im infraroten Bereich, ab 0,76 µm, werden 648 Watt/m2 eingestrahlt. Die wesentliche Einstrahlung erfolgt auch hier im Wellenlängenbereich zwischen 0,3 und 2,5 µm.
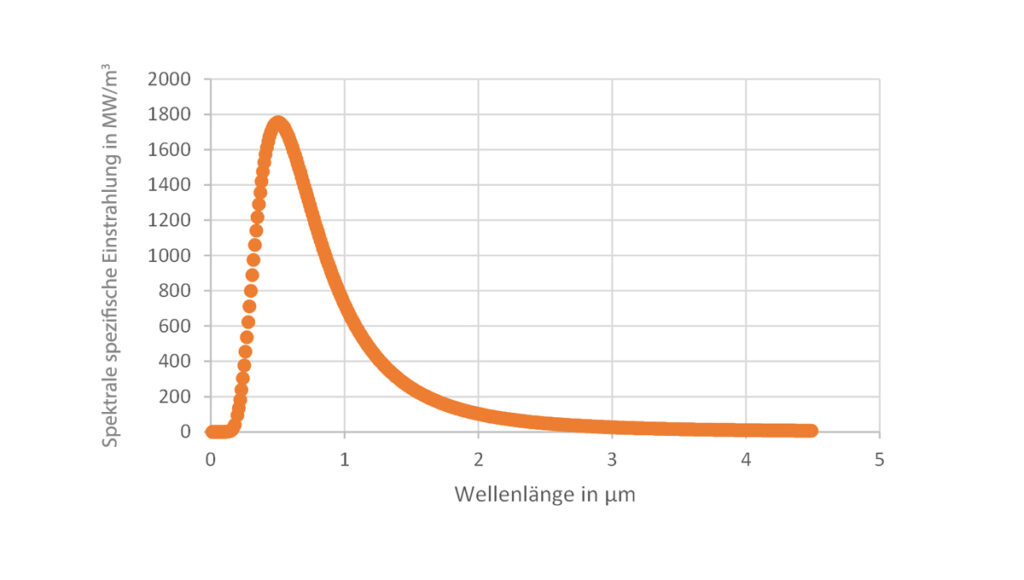
3.1. Durchlässigkeit der Erdatmosphäre
Beim Durchgang unterliegt die von der Sonne ausgehende Strahlung dem Einfluß der Atmosphäre. Die in der Atmosphäre befindlichen Moleküle streuen, absorbieren oder reflektieren die Strahlung. Bei der Absorption wird Strahlungsenergie auf das absorbierende Molekül übertragen. Bei der Streuung erfolgt eine Richtungsänderung der Strahlung, verbunden mit einem teilweisen Energieübertrag auf das streuende Teilchen.
In der folgenden Abbildung 3.1.0 ist die Durchlässigkeit als Funktion der eingestrahlten Wellenlänge im Wellenlängenbereich 0,5 bis 2,5 µm für eine klare Atmosphäre bei senkrechtem Lichteinfall dargestellt. Erkennbar sind Wellenlängenbereiche mit hoher Transmission, sog. atmosphärische Fenster. Die maßgeblichen Fenster für die wesentliche solare Einstrahlung im Wellenlängenbereich 0,3–2,5 µm liegen zwischen 0,3–1,3 µm, 1,6–1,9 µm und 2–2,5 µm.7
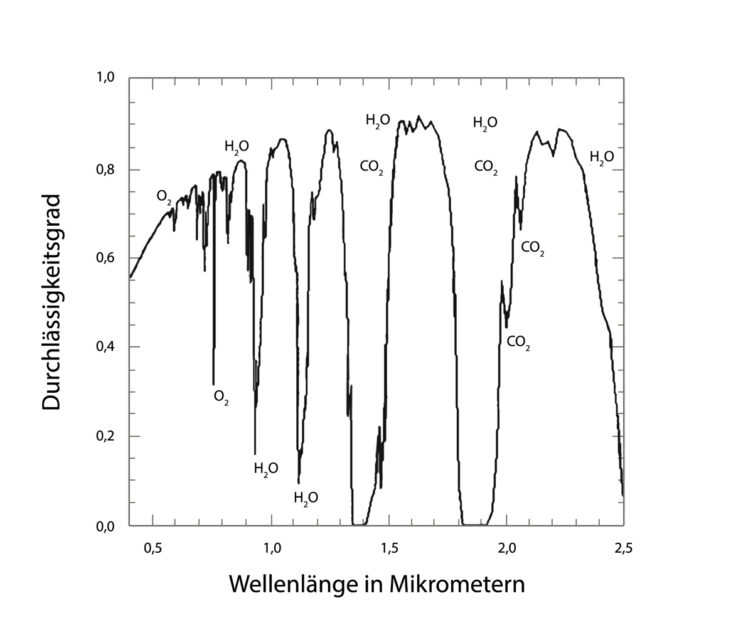
Durch die Absorption gehen im visuellen Bereich des Strahlungsspektrums (Wellenlängenbereich zwischen 0,4–0,76 µm) ungefähr 120 Watt/m2 der einfallenden Strahlung verloren. Der Verlust im Wellenlängenbereich von 0,76 µm bis 2,5 µm beträgt ungefähr 160 Watt/m2, so daß sich der Gesamtverlust durch Absorption und Streuung an Gasmolekülen auf ungefähr 22 Prozent summiert.
3.2. Reflexion der Erdoberfläche
Wie Abbildung 3.2 zeigt, besteht ein beträchtlicher Unterschied in der Reflexivität verschiedener Erdoberflächen in Abhängigkeit von der Wellenlänge der auftreffenden Strahlung.8 Im sichtbaren Bereich der solaren Einstrahlung liegt die Reflexivität der Erdoberfläche unter 20 Prozent, nur die Sandwüste erreicht Werte bis zu 30 Prozent. Deutlich unterscheidet sich die Reflexivität einer grünen Vegetation, die vor allem im nahen Infrarotbereich bei ungefähr 70 Prozent liegt, von derjenigen einer trockenen Vegetation oder eines Straßenpflasters mit einer Reflexivität von ungefähr 25 Prozent. Dabei wurde als Straßenpflaster keine Asphaltschicht angenommen, für die die Reflexivität mit derjenigen des Wassers vergleichbar ist, die im Wellenlängenbereich 0,4 bis 2,5 µm weitgehend konstant bei 12 Prozent liegt.
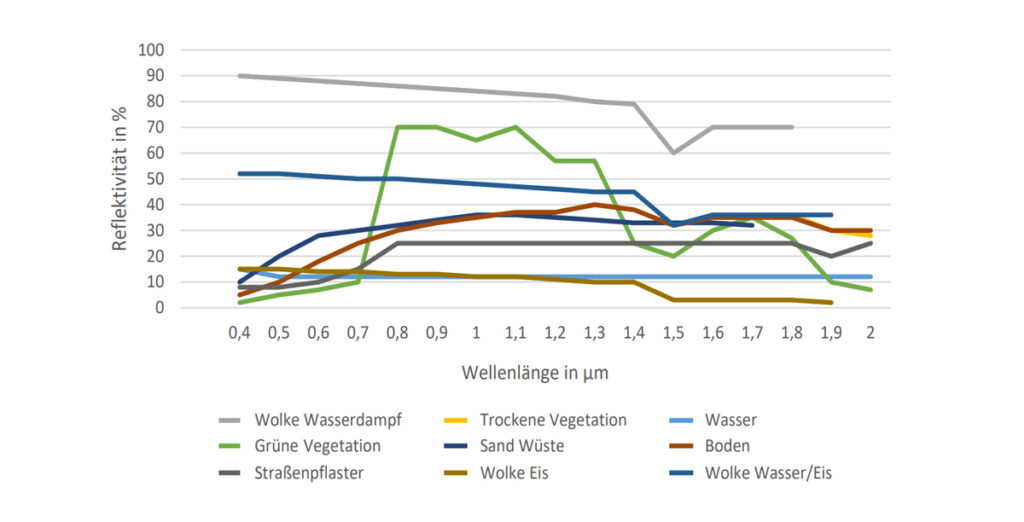
Die hohe Reflexivität des Schnees, die etwa der der Wolke aus reinem Wasserdampf entspricht, spielt nur eine geringe Rolle, da vornehmlich die Polregionen mit ihrem flachen Strahleneinfall mit Schnee und Eis bedeckt sind.
Für die Reflexivität einer Bewölkung, die zu 50 Prozent aus Eiskristallen und 50 Prozent aus kleinen Wassertropfen besteht, kann im Mittel ein Wert von 50 Prozent angenommen werden.
Für das Jahr 1986 gibt die ISCCP einen Wert von 27 Prozent für die gemittelte Reflexivität der Landflächen der Erde sowie eine gemittelte Reflexivität von 12 Prozent für die Ozeane an. Für die Gesamtreflexivität der Erdoberfläche ergibt sich daraus für 1986 ein Wert von 16 Prozent.9
Ausgehend von diesen Werten und dem um ungefähr 8 Millionen km2 höheren Waldanteil im Jahr 1750 kann für das Jahr 1750 mit einer Reflexivität der Landflächen von ungefähr 30 Prozent gerechnet werden. Die Gesamtreflexivität der Erdoberfläche könnte im Jahr 1750 bei 17,5 Prozent gelegen haben.
Durch Umgestaltung der Erdoberfläche von 1750 bis 1990 sank ihre Reflexivität gegenüber 1750 um 1,5 Prozent. Seit 1990 sind weitere 4 Millionen km2 Wald gerodet worden, davon allein 2 Millionen km2 tropischen Regenwaldes, wodurch sich die Reflexion der Landfläche auf ungefähr 26 Prozent reduziert hat. Falls diese Entwicklung ungebremst weitergeht und die Versiegelung der Erdoberfläche die für 2050 hochgerechneten 4 Millionen km2 erreicht, kann für das Jahr 2050 mit einer Gesamtreflexivität der Erdoberfläche von 15 Prozent gerechnet werden.
4. Wolkenbildung
Wolken entstehen durch Abkühlung feuchter Luft, wenn diese unter die Temperatur des Taupunktes sinkt und wenn eine ausreichende Menge an Kondensationskeimen vorhanden ist. Ohne Kondensationskeime kann die relative Feuchte, die am Taupunkt 100 Prozent beträgt, bis zu 800 Prozent steigen, ohne daß Kondensation einsetzt. Kosmische Strahlung und Aerosole verschiedenster Art wirken als Kondensationskeime, wie Abbildung 4.0 verdeutlicht, in der die Wolkenfahnen zu erkennen sind, die sich durch die schwefelhaltigen Abgase der Transportschiffe gebildet haben.

Die kosmische Strahlung ist überwiegend bei der Bildung hoher Wolken beteiligt.
Die genaue Abschätzung der weltweiten Wolkenbedeckung ist schwierig, da sie nicht nur jahreszeitlich, sondern auch über größere Zeiträume nicht konstant ist. In der Literatur angegebene Bedeckungsgrade schwanken zwischen 60 und 70 Prozent. Jonas geht von einer weltweiten Wolkenbedeckung aus, die von ungefähr 68 Prozent im Jahr 1983 auf 64 Prozent im Jahr 2016 sank.
Wolken erscheinen in den verschiedensten Formen. Die internationale Wolkenklassifikation teilt sie in 9 Wolkengattungen und in Abhängigkeit von der Höhenlage in der Troposphäre in drei Kategorien ein, hohe, mittlere und tiefe Wolken, wie Abbildung 4.1 zeigt.10
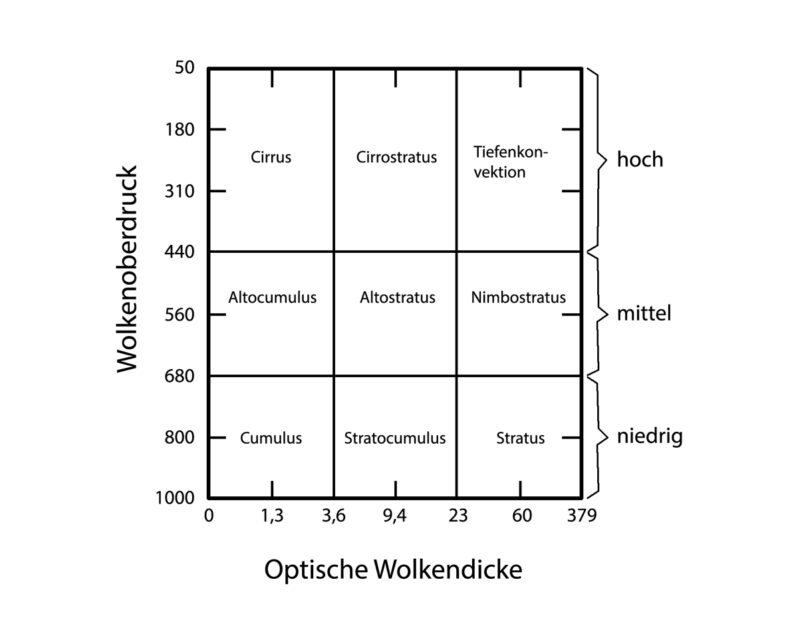
Hohe Wolken befinden sich oberhalb von 7 km Höhe und sind meist dünne, weißliche Gebilde aus Eiskristallen. Mittelhohe Wolken liegen zwischen 2 und 7 km Höhe. Sie bilden oft eine einförmige graue Schicht und bestehen aus Eiskristallen und kleinen Wassertropfen. Tiefe Wolken erstrecken sich zwischen der Erdoberfläche und etwa 2 km Höhe. Sie bestehen ausschließlich aus Wassertropfen. Aufgrund der geringen Reflexivität der Eiskristalle wird die kurzwellige Einstrahlung der Sonne im Wesentlichen an den Wassertropfen der mittleren und tiefen Wolken reflektiert.
Eine prozentuale Zusammenstellung der Wolkentypen und ihrer jeweiligen Zusammensetzung aus Eiskristallen und Wassertropfen ist der Tabelle 4.1 zu entnehmen.
Tabelle 4.1: Prozentualer Anteil und Zusammensetzung der Bewölkung (1986–1993)
| Prozent | davon Eis | davon Wasser | |
| Cumulus | 12,5 | 1,3 | 11,3 |
| Stratocumulus | 12,1 | 0,9 | 11,2 |
| Stratus | 1,9 | 0,2 | 1,7 |
| Altocumulus | 9,3 | 5,1 | 4,2 |
| Altostratus | 7,8 | 3,8 | 4 |
| Nimbostratus | 2,1 | 1 | 1,1 |
| Cirrus | 13,2 | 13,2 | |
| Cirrostratus | 5,8 | 5,8 | |
| Tiefenkonvektion | 2,6 | 2,6 | |
| Gesamtbewölkung | 67,3 | 33,9 | 33,5 |
Für die gesamte Bewölkung kann davon ausgegangen werden, daß sie sich zu 50 Prozent aus Eiskristallen und 50 Prozent aus Wassertropfen zusammensetzt.
Eine Vorstellung vom Einfluß der Wolken auf die Einstrahlung an der Erdoberfläche liefert der Strahlungsfluß an Gewittertagen. Bei voller Sonneneinstrahlung kommen über 1000 Watt/m2 an der Erdoberfläche an, ziehen dicke Gewitterwolken auf, sinkt der Strahlungsfluß leicht auf 50 Watt/m2 und weniger. Bei Dämmerung und wolkenlosem Himmel und einem Sonnenstand knapp unter dem Horizont liegt die Einstrahlung unter 0,1 Watt/m2.
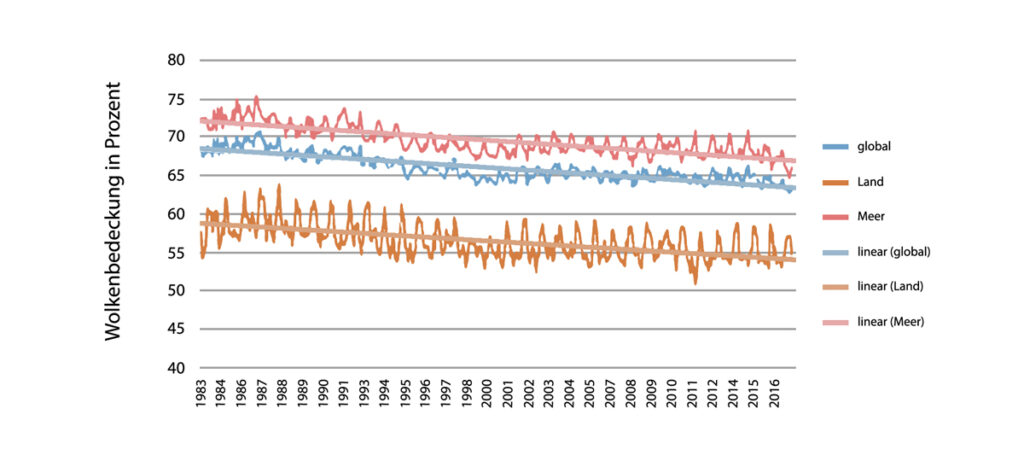
Während sich die Wolkenbedeckung zwischen 1983 und 2016 verringert hat, nahm die Durchlässigkeit der Wolken, gemessen über die Opazität von 53 Prozent auf 57 Prozent ab, wie Abbildung 4.2 zeigt.
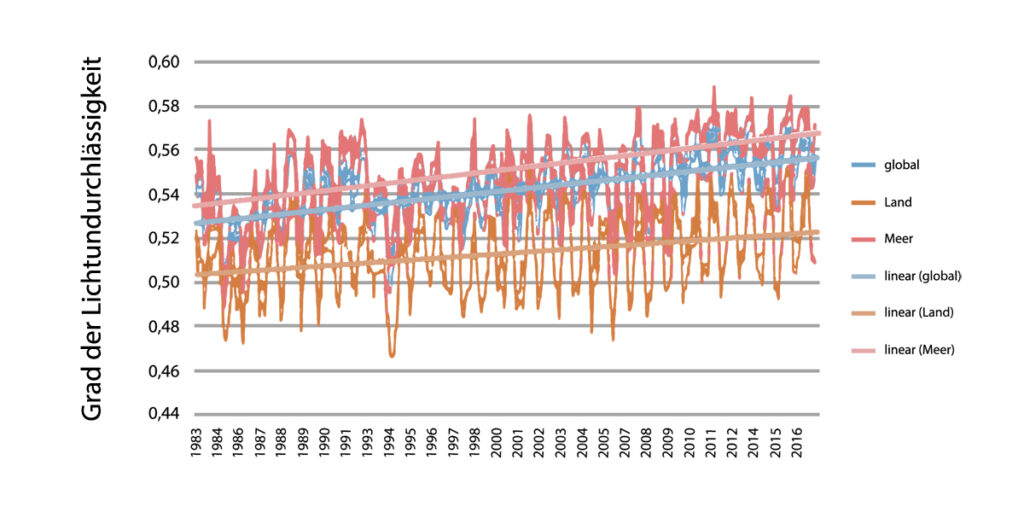
Weltweit wurde 1983 durch die Wolkenbedeckung 53 Prozent der einfallenden Strahlung reflektiert und absorbiert. Dieser Wert stieg bis 2016 auf 57 Prozent.
Einfallende Strahlung wird an der Wolkenoberfläche teilweise durch direkte bzw. mehrfache Reflexion an den Wassertropfen der Wolke zurückgeworfen, ein geringer Anteil wird absorbiert. Der Rest geht als diffuse Strahlung durch die Wolke hindurch.
4.1. Der wolkenbildende Einfluß der Aerosole
Die wesentlichen Aerosole sind Meersalz, Mineralstaub, biologische Teilchen, Ruß und Sulfat. Mineralstaub wird durch den Wind aufgewirbelt, so daß besonders in Wüstengebieten hohe Konzentrationen gemessen werden; Meersalz gelangt durch verdunstendes Sprühwasser in die Atmosphäre. Da die überwiegende Landfläche der Erde mit Lebewesen und Pflanzen bedeckt ist, gelangen Mikroorganismen (Bakterien, Pilze, Sporen) und abgeriebene zelluläre Teilchen in die Luft. Die Quellstärke der globalen Landfläche liegt in gleicher Größenordnung wie die der Wüsten und der Ozeane. Während die Aerosole aus Meersalz, Mineralstaub und biologischen Teilchen kaum durch menschliche Aktivitäten beeinflußt werden, sieht es bei Ruß und Sulfataerosolen anders aus.
Ruß ist ein Verbrennungsprodukt und stammt aus menschlichen und natürlichen Quellen. Sulfataerosole entstehen in der Atmosphäre durch die Reaktion von bei der Verbrennung freiwerdendem Schwefeldioxid (SO2) mit anderen Stoffen. Ruß und Schwefeldioxid werden aus natürlichen Quellen, wie zum Beispiel Waldbränden und Vulkanausbrüchen, im wesentlichen jedoch bei industriellen Prozessen oder Verbrennung zur Wärmeerzeugung frei. Diese Quellen sind also zum einen Teil natürlichen und zum anderen Teil menschlichen Ursprungs.
Zusätzlich zu den Aerosolen, die sich auch in vorindustriellen Zeiten, wenngleich zu geringeren Konzentrationen, in der Atmosphäre befanden, beeinflussen heute feine Rußteilchen und Sulfataerosole die Wolkenbildung. Sie wirken als Kondensationskeime und führen über die Anlagerung von Wasser zur Bildung von Wolkentröpfchen. Die hydrophile Eigenschaft der Sulfataerosole führt bereits bei üblicher Luftfeuchte von 60–70 Prozent zur Kondensation, während hydrophobe Partikel wie Ruß erst bei einer Luftfeuchte über 100 Prozent als Kondensationskeime wirken.
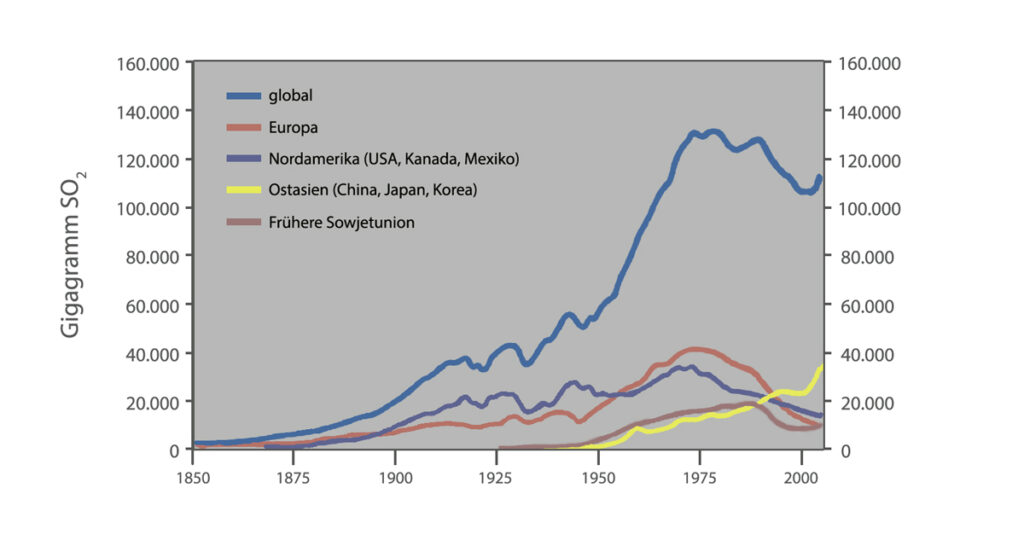
Aus Abbildung 4.3 ist ein steiler Anstieg der Schwefeldioxidemission von 1950 bis 1975 zu erkennen, der zeitlich übereinstimmt mit dem in Abbildung 1.0 dargestellten Temperaturplateau und auf eine verstärkte Wolkenbildung hinweist. Die von Jonas beschriebene Veränderung der Wolkenbedeckung kann auf die seit 1980 wirkende Reduktion des weltweiten Schwefeldioxidausstoßes aufgrund des entsprechenden „clean air act“ von 1956 zurückgeführt werden.11
5. Effektive solare Einstrahlung und Oberflächentemperatur
Die Abschätzung der Rückstrahlung von der Erde und ihrer Atmosphäre ohne klimatische Wirkung im System Erde/Atmosphäre geschieht, indem folgender Strahlungsfluß berücksichtigt wird:
Der von der Sonne kommende Strahlungsfluß wird durch Absorption in der Atmosphäre bis zum Auftreffen auf die Wolkenschicht geschwächt und danach teilweise direkt oder nach einer Mehrfachreflexion als diffuse Strahlung in den Weltraum reflektiert (S1).
Der nicht in Richtung Weltraum reflektierte Teil geht über Mehrfachreflexion und Absorption durch die Wolke hindurch und trifft nach weiterer Schwächung durch Absorption in der Luftschicht, verstärkt durch den nicht durch die Wolken geschwächten Anteil des Strahlungsflusses, auf die Erdoberfläche, von der er dann entsprechend der Reflexivität der Erdoberfläche teilweise reflektiert wird.
Der reflektierte, von der Erdoberfläche kommende Strahlungsfluß trifft nach Schwächung durch Absorption in der Atmosphäre auf die Unterseite der Wolken und wird dort wieder teilweise reflektiert. Der nicht reflektierte Strahlungsfluß durchdringt diese, geschwächt durch die Absorption in der Wolke, und erreicht, wieder verstärkt durch den nicht von den Wolken geschwächten reflektierten Strahlungsfluß, mit den Absorptionsverlusten der Atmosphäre den Weltraum als Beitrag (S2) zur Gesamtreflexion der Erde.
Der geringe, von der Unterseite der Wolken zurückgestrahlte Anteil des Strahlungsflusses wird nach Schwächung durch die Atmosphäre wieder von der Erdoberfläche reflektiert und liefert den Beitrag S3 zur Gesamtreflexion SR.
Da die Erde keine wesentlichen anderen Energiequellen besitzt, bestimmt die Gesamtreflexion des Systems Erde bzw. der vom System aufgenommene Strahlungsfluß der Sonne die Strahlungsgleichgewichtstemperatur.
Anhand von
SA = SE – SR ,
wobei SR die reflektierte Strahlung von der Kreisscheibe Erde und SE die Einstrahlung angibt, errechnet sich aus dem Stefan-Bolzmann-Gesetz die Temperatur TM, die Temperatur der auf eine Ebene geschrumpften Masse der Atmosphäre zu:
TM = (SA/(4 · σ))1/4 [5.1]
Das Einsetzen von Gleichung 5.1 in Gleichung 2.2.1 ergibt:
T0 =(SA/(4 · σ))1/4 · eP0 · g (HM – H0) · (κ – 1)/(P0 · κ) [5.2]
Die Gleichung 5.2 stellt eine Kopplung von thermischer und potentieller Energie sowie Strahlungsenergie für die Berechnung der Oberflächentemperatur der Erde dar.
In der Tabelle 5.2 sind die berechneten Werte für die Temperatur der Erdoberfläche in Abhängigkeit von den in den vorhergehenden Kapiteln beschriebenen Eigenschaften des Systems Erde aufgeführt.
Tabelle 5.0: Annahmen für die Berechnung der Strahlungsgleichgewichtstemperatur
| Beispiel | Bewölkung (in %) | Reflexion Erdoberfläche (in %) | Reflexion der Bewölkung (in %) | Absorption der Bewölkung (in %) | Absorption der Atmosphäre (in %) |
| 1 | 68 | 16 | 50 | 3 | 22 |
| 2 | 68 | 17,5 | 50 | 3 | 22 |
| 3 | 68 | 15 | 50 | 3 | 22 |
| 4 | 64 | 16 | 51 | 6 | 22 |
| 5 | 64 | 17,5 | 51 | 6 | 22 |
| 6 | 64 | 15 | 51 | 6 | 22 |
Tabelle 5.1: Reflektierte Strahlungsflüsse
| Beispiel | In den Weltraum von den Wolken reflektierter Strahlungsfluß durch Sonneneinstrahlung → S1 (in W/m2) |
In den Weltraum von der Erde direkt reflektierter Strahlungsfluß durch Sonneneinstrahlung → S2 (in W/m2) |
In den Weltraum von der Erde reflektierter Strahlungsfluß durch Wolkenreflexion → S3 (in W/m2) |
| 1 | 367,6 | 66,8 | 2,7 |
| 2 | 367,6 | 75,3 | 3,5 |
| 3 | 367,6 | 62,7 | 2,4 |
| 4 | 352,9 | 67,9 | 2,8 |
| 5 | 352,9 | 74,2 | 3,4 |
| 6 | 352,9 | 63,6 | 2,5 |
Tabelle 5.2: Strahlungsgleichgewichtstemperaturen
| Beispiel | Von der Erde als Kreisfläche absorbierter Strahlungsfluß → SA (in W/m2) | Von der Erde als Kugelfläche absorbierter Strahlungsfluß → S (in W/m2) | Strahlungsgleichgewichtstemperatur TM (in K) | Temperatur der Erdoberfläche T0 (in K) | Temperatur der Tropopause TT (in K) |
| 1 | 927,9 | 232 | 252,9 | 288,32 | 221,56 |
| 2 | 918,6 | 229,7 | 252,3 | 287,59 | 220,99 |
| 3 | 932,3 | 233,1 | 253,2 | 288,66 | 221,81 |
| 4 | 941,4 | 235,4 | 252,8 | 289,36 | 222,35 |
| 5 | 934,5 | 233,6 | 253,4 | 288,83 | 221,94 |
| 6 | 946 | 236,5 | 254,1 | 289,71 | 222,62 |
Ausgehend von einer Wolkenzusammensetzung, wie sie in Tabelle 4.2 dargestellt ist, können die Ergebnisse der Berechnung wie folgt zusammengefaßt werden:
Ausgehend von einer Wolkenbedeckung von 68 Prozent, wie sie für das Jahr 1986 gemessen wurde, sowie einer Wolkenzusammensetzung, wie sie in Tabelle 4.2 dargestellt ist, einer Opaziät der Bewölkung von 53 Prozent, die sich aus 50 Prozent Reflexivität an der Wolkenoberfläche und 3 Prozent Absorption in den Wolken zusammensetzt, sowie einer Reflexivität der Erdoberfläche von 16 Prozent ergibt sich eine Rückstrahlung des Erdsystems von 437,1 Watt/m2 und eine Temperatur der Erdoberfläche von 288,3 K. Durch Veränderung der Reflexivität der Erdoberfläche auf 17,5 Prozent ergibt sich eine Rückstrahlung des Erdsystems von 446,4 Watt/m2 und eine Temperatur der Erdoberfläche von 287,6 K.
Bei einer Verringerung der Wolkenbedeckung auf 64 Prozent, einer Opazität der Bewölkung von 57 Prozent sowie einer Reflexivität der Erdoberfläche von 16 Prozent ergibt sich eine Rückstrahlung des Erdsystems von 423,6 Watt/m2 und eine Temperatur der Erdoberfläche von 289,4 K. Durch Veränderung der Reflexivität der Erdoberfläche auf 17,5 Prozent steigt die Rückstrahlung des Erdsystems auf 430,5 Watt/m2 und führt zu einer Temperatur der Erdoberfläche von 288,8 K. Bei einer weiteren Reduktion der Reflexivität (Erdoberfläche auf 15 Prozent, Aerosole plus 1 Prozent) würde die Temperatur der Erdoberfläche auf 290,3 K steigen.
6. Zusammenfassung
Die Sonne ist die wesentliche Energiequelle der Erde. Sie bestrahlt die Erde mit einer Leistung von durchschnittlich 1365 Watt/m2, die jedoch nicht vollständig energiewirksam das System Erdoberfläche/Atmosphäre erreicht. Bewölkung, Wolkenstruktur und Reflexivität der Erdoberfläche beeinflussen die Strahlungsleistung, die ohne Einwirkung auf die Temperatur des Systems Erde wieder in den Weltraum abgestrahlt wird.
Entscheidend für die Temperaturverhältnisse auf der Erdoberfläche ist die Energie, die das System Erde einschließlich seiner Atmosphäre aufnimmt.
Die Atmosphäre steht unter dem Einfluß der von der Erde ausgeübten Massenanziehung, der thermodynamischen Gesetze eines realen Gasgemisches sowie des Strahlungseinflusses der Sonne. In dem System Erdoberfläche/Atmosphäre stellt die Summe aus thermischer, potentieller und Strahlungsenergie eine Erhaltungsgröße dar.
Die unabhängige Betrachtung einzelner Energieformen bei der Abschätzung klimatischer Änderungen ist nicht zulässig.
Bei einer Erdkugel, deren Atmosphäre durch andere als die Gravitationskräfte festgehalten wird, hätte die Luftschicht eine von der Höhe unabhängige Dichte. Sie wäre überall gleich und hätte überall die gleiche Temperatur TM = 253 K, die Strahlungsgleichgewichtstemperatur, die gleich der Temperatur in der Halbwertshöhe HM = 5500 m ist.
Wird die Gravitation „dazugeschaltet“, so erfolgt durch die Schwerkraft eine Dichte- und Druckzunahme in Richtung Erdmittelpunkt und eine Dichte- und Druckabnahme in Richtung der oberen Grenze der Atmosphäre. Dieser Vorgang entspricht einer adiabatischen Expansion nach oben und einer adiabatischen Kompression in Richtung des Erdmittelpunktes. Es kommt in Richtung der Erdoberfläche zur Erwärmung von 253 K auf 288 K und in entgegengesetzter Richtung zur Abkühlung von 253 K auf 222 K bei einer Höhe von 11.100 Metern.
Durch die adiabatische Kompression unter dem Einfluß der Schwerkraft erhöht sich die Temperatur der Luft an der Erdoberfläche von 253 auf 288 Kelvin. Die Temperatur an der Troposphärengrenze bei ungefähr 11.000 m reduziert sich auf 222 Kelvin.
Es ist also keine Gegenstrahlung erforderlich, um die Temperaturdifferenz zwischen der Strahlungsgleichgewichtstemperatur und der gemessenen gemittelten Temperatur der Erdoberfläche zu erklären.
Die Strahlungsgleichgewichtstemperatur, die sich aus der Differenz der solaren Einstrahlung und der von Wolken und Erdoberfläche reflektierten Strahlung berechnen läßt, ist die entscheidende Größe für die Berechnung der Temperatur auf der Erdoberfläche.
Auf der Basis gemessener Werte für die Wolkenbedeckung und ihrer Zusammensetzung und ihrer Reflexivität, des Absorptionsverhaltens der Atmosphäre und der Reflexivität der Erdoberfläche ergeben sich Temperaturen für die Erdoberfläche, die im Bereich der gemessenen, gemittelten globalen Temperatur liegen.
Ausgehend von einer Wolkenbedeckung von 68 Prozent und einer Reflexion der Erdoberfläche von 16 Prozent sowie einer Opazität der Bewölkung von 53 Prozent, wie sie dem Systems Erdoberfläche/Atmosphäre im Jahr 1980 zugeordnet werden können, ergibt sich eine Temperatur der Erdoberfläche von ungefähr 288,3 Kelvin. Für das Jahr 2000 mit der geringeren Wolkenbedeckung von 64 Prozent und der Opazität von 57 Prozent liegt die berechnete Temperatur bei 289,4 K also bei einer um 1,1 K höheren gemittelten Globaltemperatur. Im Vergleich zur Darstellung Abbildung 1.0 stellt dieses Resultat eine gute Übereinstimmung dar, wenn berücksichtigt wird, daß die Einstellung des Temperaturgleichgewichts im Jahr 2000 noch nicht abgeschlossen war, 2020 bereits eine Globaltemperatur erreicht war, die um 1 K über derjenigen von 1980 lag und immer noch steigt.
Die durch zivilisatorische Aktivitäten bedingte Umgestaltung der Erdoberfläche in der kurzzeitigen Vergangenheit führte zu einer deutlichen Verringerung der Reflexivität der Erdoberfläche von 17,5 Prozent im Jahr 1750 auf heute ungefähr 16 Prozent. Bei gleichbleibender Wolkenbedeckung von 68 Prozent ergibt sich für die Temperatur der Erdoberfläche im Jahr 1750 ein Wert von 287,6 Kelvin, der ungefähr 0,7 K niedriger ist, als die gemittelte globale Temperatur im Jahr 1980.
Die Ausführungen zeigen, daß das Erdklima nur konstant gehalten werden kann, wenn der Energieeintrag in das System Erdoberfläche/Atmosphäre über große Zeiträume konstant ist. Änderungen in der Energieaufnahme führen zu einem geänderten Gleichgewichtszustand und damit zu einer „Klimaänderung“.
Durch Veränderungen des Reflexions- und Absorptionsverhaltens des Systems beeinflußt der Mensch das Klima auf der Erde. Jegliche Aktivität, die die Reflexion der Erdoberfläche oder die Wolkenbedeckung verringert, führt zu einer Erhöhung der Gleichgewichtstemperatur. Dazu gehört die Rodung von Wäldern, die Umwandlung grüner Flächen in Flächen geringerer Reflexivität, wie Asphalt, Beton und Dachflächen, sowie die Umwandlung von Wiesen in schwarze Photovoltaik-Felder.
Nicht das Kohlendioxid ist die treibende Kraft einer Klimaänderung sondern die anhaltende Verringerung der Reflexivität der Erdoberfläche durch den Menschen ist die Ursache für eine höhere Gleichgewichtstemperatur des Systems Erde/Atmosphäre.
Kohlendioxid ist eine völlig ungeeignete Regelgröße für eine Klimabeeinflussung.
Auch wenn die anthropogene Kohlendioxiderzeugung völlig beendet wird, wird die globale Temperaturerhöhung weitergehen, solange die Menschheit nicht aufhört, ihren Planeten als Strahlungsabsorber umzugestalten.
Die massiven Eingriffe in die Reflexivität der Erdoberfläche, wie sie vor allem durch den verstärkten Ausbau der Solarenergie im Rahmen der „erneuerbaren Energien“ zu erwarten sind, werden die globale Temperaturerhöhung eher beschleunigen als verringern. Auch wenn medizinische Gründe entscheidend sind, sollte jeder „clean air act“ auf seine negative Rückkopplung auf die Wolkenbildung und damit auf die Globaltemperatur überprüft werden.
Auch im Hinblick auf die ständig steigende Weltbevölkerung sind die Bemühungen der westlichen Welt, die Entkarbonisierung der Weltwirtschaft durchzusetzen, eher als eine Doktrin zur Sicherung politischer Einflußnahmen zu sehen, als ein Wegbereiter für das Zusammenleben von zukünftig 11 Milliarden Menschen auf der Erde.12
Dr. Jürgen Langeheine, Autor des Buches Energiepolitik in Deutschland – das Geschäft mit der Angst, ist promovierter Physiker und war hochrangiger Manager der BASF.
Fußnote(n)
- P. R. Goode et al., 2021, „Earth’s Albedo 1998–2017 as Measured From Earthshine“, 48, Geophysical Research Letters, 48, e2021GL094888, https://doi.org/10.1029/2021GL094888[↩]
- Siehe www.worldindata.org.[↩]
- Siehe www.regenwald-schuetzen.org.[↩]
- N. Ramakutty, J. A. Foley, 1999, „Estimating Historical Changes in Global Landcover“, Global Biological Cycles 13 (4), 997–1027[↩]
- Siehe scinexx.de und kompost.de.[↩]
- J. Langeheine, 2012, Energiepolitik in Deutschland – das Geschäft mit der Angst, Athene Media-Verlag ISBN 978-3-86992-054-2[↩]
- Die Extinktion – astro.uni-jena.de[↩]
- Zusammenstellung der Reflexivitäten aus verschiedenen Quellen: 1. ASTER- Datenbank (1992); 2. „Eigenschaften der Wolken im VIS/NIR“, Institut für Raumfahrtsysteme, www.irs.uni-stuttgart.de[↩]
- M. O. Jonas, „Clouds independently appear to have as much or greater effect than man-made CO2 on radiative forcing“, World Journal of Advanced Research ans Reviews, 2022, 14(02), 564–572[↩]
- W. B. Rossow, R. A. Schiffer, 1999, „Advances in Understanding Clouds from ISCCP“, Bulletin of American Meteorological Society, Vol. 80, No. 11[↩]
- Siehe 9.[↩]
- J. Langheine, 2022, „Bevölkerungswachstum, große Transformation und globale Verschuldung“, FUSION, 43, 02/2022, 51–60[↩]
